Оглавление:


























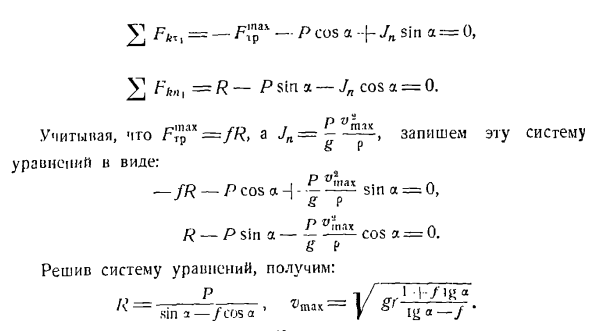













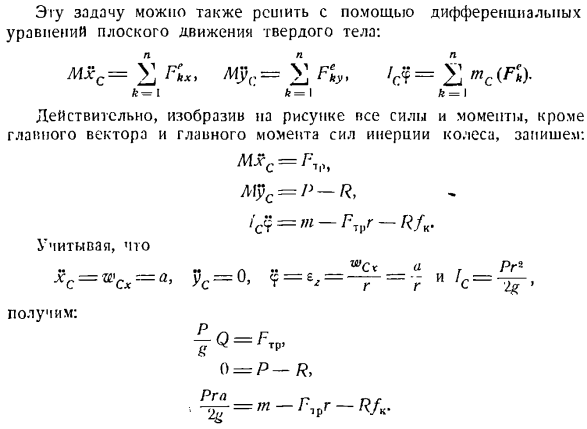

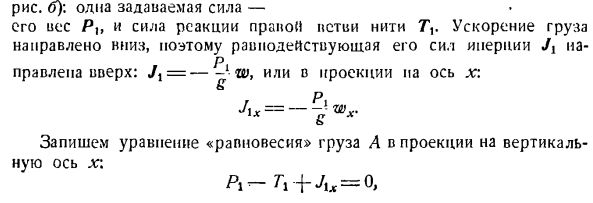







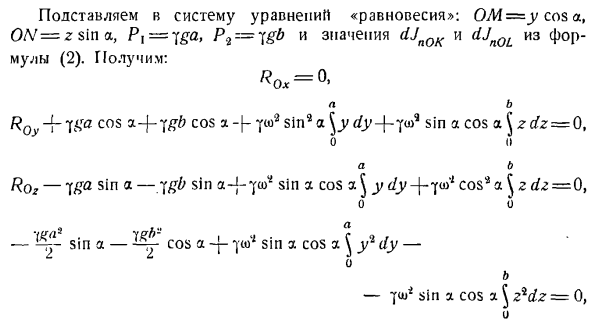

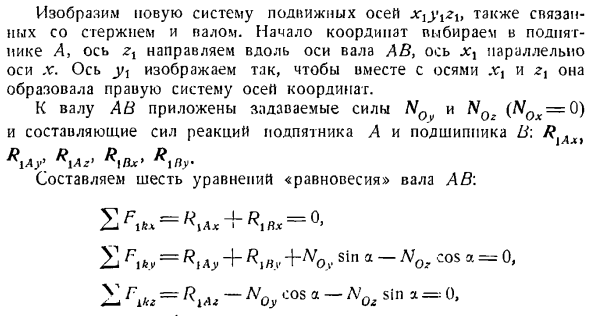
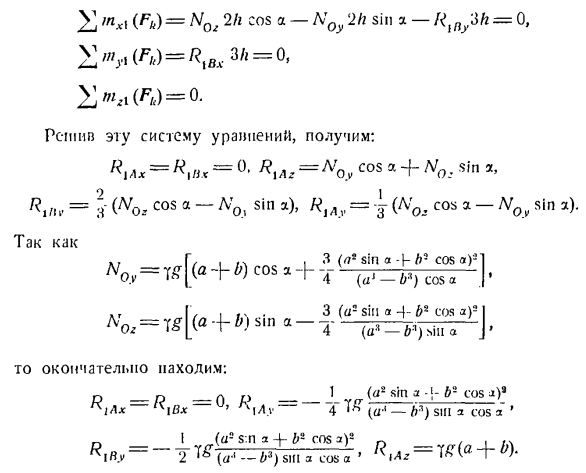







Метод кинетостатики
- Кинетическая статика 1e. сила инерции. Начало силы инерции для основного вектора и основного момента. При взаимодействии двух свободных материальных точек к одной из них прикладывается сила Fx, называемая действием, а к другой-сила Fb, называемая реакцией. Со стороны точки массы B действие прикладывается к точке массы A (рис. 145), где получается ускорение w, а позже оно называется «ускорением r». Вт * in_F / Дж Точка B (y1, или^ * Сообщите, что ускорение является точным」
Материальная точка А 145 на рисунке. Это называется ускорение. «Ускорение^к точке В, реакция прикладывается со стороны»ускорения» точки А. На принципе равенства действия и реакции、 Ф■= — / В Согласно Основному закону динамики, действие Fx = mwt, поэтому реакция будет равна/ g9 = — mw. Реакция называется инерционной силой и обозначается Дж.а модуль ее ускорения направлен в противоположную сторону от ускорения точки А,
Так, в случае свободных материальных точек величина инерционной силы «равна произведению массы ускорения*точки А Людмила Фирмаль
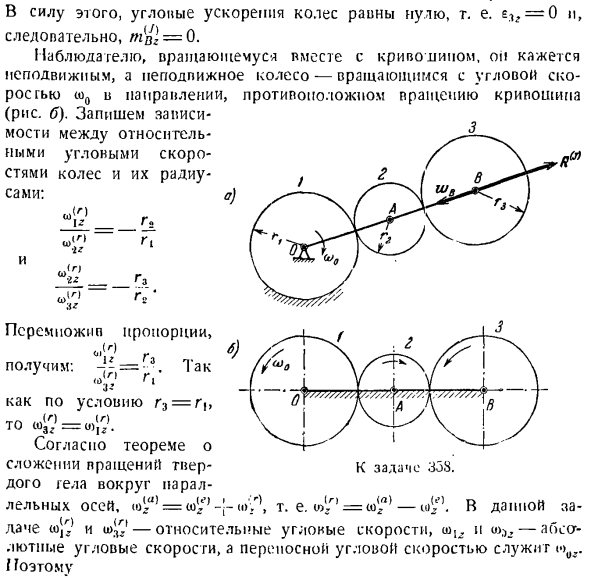
которое приложено к» ускорению » точки Б. Благодаря этому ускорение угольного ускорительного колеса равно нулю, то есть e ^ = 0、 Так что m [Ц= 0. Для наблюдателя, вращающегося вдоль кривой, это выглядит так, как будто движения нет, а колесо без движения-оно вращается с угловой скоростью (o0 (B) в противоположном направлении вращения кривошипа). iz_ _ _ _ Г3 о > [п г«’ «Это» Коэффициент умножения 、 Да.、 — }£=■■?。Так… Условие r3 = r (>тогда». — Салютная угловая скорость, а переносная угловая скорость равна/ 0) (дя = ву-у WFL., =- (йог рассматривая to, y =ω, σ> 3,=(σ1,
но по гипотезе колесо 1 не работает, то есть ω1= 0, а следовательно σ>,.= 0.Это означает, что колесо 3 совершает круговое поступательное движение. Как известно, при поступательном движении твердого тела сила инерции уменьшается в результате приложения к центру тяжести твердого тела./ < * г> = — а \ W, где W-ускорение любой точки твердого тела. Поскольку точка B является конечной точкой кривизны в то же время, легко определить ускорение точки B
- в колесе. Если% является постоянным, то WN = wlu-= \ LV ускорение wn от B до O(rns. А) быть directed. As в результате реалист: и сила инерции RJ \ 3. центр тяжести колеса закреплен, вдоль Оби п Ось вращения O и модуль R (.) = −3 / 0 /.отель JW-. Проблема 369.План поворачивается вокруг неподвижной оси O, перпендикулярной плоскости фигуры. Определяет главный вектор и главный момент инерции материальной точки На виде в плане. С точкой O в качестве
центра редукции вектор e направлен перпендикулярно плоскости фигуры. Решение. укажите ось z на B. То есть она перпендикулярна плоскости изображения. Возьмите любую точку K на виде в плане. . it состоит из、 Сус — » х = гы = = ОК —расстояние от точки K до оси вращения О (направления осей M и N показаны на рисунке). Согласно ускорению, wnb%w. j. и wk-это сила инерции материальной точки, направленная в противоположном
Ускорение точки K wk wk ее центростремительная wnk и вращательная составляющая w Людмила Фирмаль
направлении: Jn!{J. u и Jk. Центробежная сила инерции: Jnk = -wwnk. проекция на ось n: Jnk = — / n ^ n) 4.Вращательная сила инерции= — tnkwxk. проекции на ось X: Jzk = — pkgkkg2.Суммарная инерционная сила: В JK = — mkwk. Его модуль: Jk = = mkrk | / e * — J-от 4. По определению основного вектора инерционных сил: V (.) = ^ Jk \ По этому вопросу, 359. н Предполагая, что Jk = — tikwk, вы можете использовать V (y> = — ЩИ > к- Н = 1 Используйте формулу, приведенную в главе IX 1°2. н Х rnkWh — I-масса системы
в материальной точке, WC- Ускорение инерциального центра системы, получим: н Г (г)= — в mkwk = — мЗв, к-я т. основной вектор сил инерции направлен в противоположную сторону к ускорению ruJc центра тяжести C на виде в плане. В зависимости от условия задачи, если точка O центрирована на торможении, то в этой точке должна быть приложена сила V(J) (см. рисунок).По модулю= = rf \ / r1 -} — to1, где rf-расстояние от оси O до центра Основным вектором силы тяжести С, инерционных сил, является модуль вида сверху В (к)=
Мик / ЕІ + В4. Приступим к расчету главного момента инерции / / материальной точки плоской фигуры. Это «против точки о«.Это будет равно сумме моментов всех сил инерции для данной точки. «(О = Т » О (А)= Ж] М0 (Jnk)-[- с / ч0 б = я и= и к = я Момент центробежной силы инерции в точке О равен нулю. н Один И так оно и есть.: ж] т0 (/»)= в 1 Фе = 1 Jxk = — Mkrke2t Н. Н. Н. mkri = — значения i0 <Lzy л = я фут = я н Где Iq = V] / ng \ — момент инерции плана этажа. Это=я Оси о, перпендикулярной к плоскости. Так…
rrto ==-/ о£р- Символ главного момента / / th противоположен символу предсказания ускорения углеводорода e. Проблема 360.Используйте результаты предыдущей задачи для определения основного вектора и главного момента инерции плоского чертежа, а также центра тяжести C плоского чертежа в качестве центра сжатия. Решение. И сила вый \показывается. Это относится и к точкам о, равным горе главного века инерции forces. In решая предыдущую задачу, она была
получена следующим образом: АУ)= — КТМ, т(о = — 10л. Давайте сделаем переход от старого центра замедления O к новому центру замедления C. To для этого покажем 2 вектора равновесия в точке C: V’KJ) и Vr < — / > = — V ’(J>.Теперь сила инерции в (J) прилегает к центру тяжести плана. В этом случае, пара дополнительных инерционных сил、 б) Точке О, и силы, [Дж).Добавлена тяжелая пластина arm h (.= Gc sin a. таким
образом, момент пары добавленных инерционных сил равен Л * ю по этому вопросу. В (к) СЖК = в (к) радиоуправляемый грех = = ] / е’2-й — с> 4 грех А. Основной момент инерции для нового центра торможения с равен сумме момента силы инерции для старого центра торможения О и момента добавленной пары сил инерции. 1, » ( ’ ) _ ЭйДжей) / Л С =тогда в пиар =- — — Г-н C] / Е *(О4 грех. Восп. Р, называется рис. б, мы найдем: Так… ««с» = — + МРТ™ТМ»=-/о», + Afrfc,= =
— е (/о-Afrt). При применении теоремы llhetliepa:/ 0 = / r — [.- Эйр, мы находим, что / 0- — Х4 = / с- Следовательно, момент инерции утюжка/ Т равен Проблема 361.Линейка эллипсографа AB движется по крошизе от ОС, вращающейся с постоянной угловой скоростью o>
0. Определить главный вектор и главный момент инерции прямой AB массы P и длины/и считать, что она является равномерной прямой Ядра; ОС = АС = СВ = Решение. Линия АВ совершает плоское движение. Таким образом, его инерционная сила сводится к силовой паре, равной основному ikgor V { ’ \ , а момент равен основному моменту mc. Сила, равная основному вектору инерционной силы V (J \приложена к центроиду линейки, а ускорение центроида C направлено
в направлении, противоположном ускорению Wc: VlJ)= — Mwc-центроид C линии AB является в то же время концом ползучести ОС, поэтому если угловая скорость центростремительной силы, ускорение wr%, направлена от С до O. As в результате основной вектор V (7) силы инерции направлен от оси вращения о вдоль криволинейного шипа OS. In абсолютное значение, оно равно Uy> = Mo> s. wc = wc =; OS / w $ = find: * Основной момент инерции линии АВ определяется по формуле m {Q] = — / seg. Где Момент
инерции линии АВ к оси через центроид с перпендикулярен неподвижной плоскости, Е2-проекция углового ускорения линии АВ на ось z, перпендикулярную плоскости фигуры. Определив мгновенную скорость центра и положение линейки как точки пересечения перпендикуляров, восстановленных из точек А и в до соответствующей скорости, вы увидите угловую скорость линейки АВ. Скорость точки C, которая является конечной точкой кривошипа ОС, равна vc = \ OC \ u); в то время как скорость точки C, которая находится на линии AVU, является формулой vc = jC£Р;
u>.Итак, f Co? 01 и > = OS / т. е. / ОС’И о)= В0. Так как OC = CiP=, то угловая скорость линейки AB будет равна (o =ω0.Таким образом, угловое ускорение линейки будет равно нулю. Если при движении несвободной материальной точки ее траектория предопределяется наложенной на эту точку связью, то действие со стороны наложенной связи прикладывается к материальной точке»ускоренной», заменяя в этом случае»ускоренную» точку. Основываясь на принципе эквивалентности действия и реакции, реакция применяется к соединению из материальной точки, называемой силой инерции J
. так как Fi= mw и F-2 = — Fx, J = Fq = — mw. Так, при равномерном движении кольца а вдоль проволоки в траектория кольца а, являющаяся точкой»ускорения», предопределяется проволокой, являющейся связью. Кольцо а приобретает центростремительное ускорение под действием силы Du, приложенной к соединению со стороны провода. Основываясь на принципе уравнения действия и реакции, сила инерции J (рис.140), называемая реакцией/ 7,
прикладывается к соответствующей точке провода. Н = Дж Фигура е =-^ н- = 0, следовательно, е ^ =0.Поэтому главный момент силы Иер-книги подряд ранен пулями. т {ы— Это означает, что сила инерции точки На прямой сводится к результирующей силе, равной основному вектору силы инерции. Проблема 362.Определите главный вектор
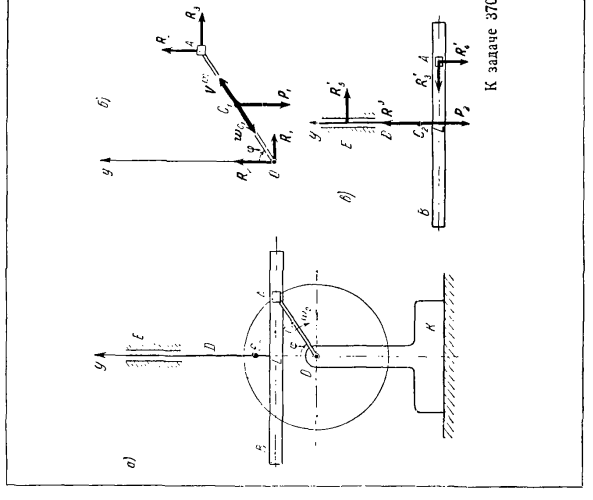
и главный момент инерции шестерни 2 во внутренней шестерне С неподвижной шестерней. Колесо 2 с массой P и радиусом r устанавливается во время работы кривошипом OL = 2r. этот кривошип имеет в данный момент угловую скорость o> 0 и угловое ускорение* E0.Колесо 2 считать однородным сплошным диском. Решение: колесо 2 делает плоское motion. In в этом случае основной вектор силы инерции V (J) равен、
Рений равен wA и p В {дл = — * Вт.. W после. = г, л, л. Ол = г −1 П)} и ОА = ’ 2Д в. (См. диаграмму а). Основной момент инерции колеса 2 имеет знак, противоположный проекции углового ускорения、 (Я) т л = — / le2g. Для определения углового ускорения е.. сказал он. Колесо 2 использует мгновенный центр скорости c7.Локус точки-это гипоциклоид, касательная, которая направлена вдоль кривошипа
в точке. Поверните ось m вдоль оси N с помощью кривошипа 0.4-WGP перпендикулярно оси m находится на оси c, поэтому проекция wgp на ось n равна нулю. =0.(2) Голы: 362 Теперь получим точку D полюса и определим ускорение. = З А + Ассоциации + + Ш&А ’ Мы проектируем это векторное уравнение (см. Рисунок B) на оси n и используем уравнение (2), чтобы получить: + =(3) «$q # 1 = | AP \ tu = n, lgt a w, An = — [OA | gog = — 2ge0r>и когда вы присваиваете эти
значения выражению (3), это выглядит так: (4 )) «Момент инерции колеса 2 относительно оси а, перпендикулярной его плоскости、 П Г2 ’Л = М£ 0 ’) Если вы присвоите r + 2 в уравнении (4) и 1L в уравнении (5) к (0), вы получите: 2°.Кинетопический метод. Метод кинетической статики называется формальным методом, в котором уравнения движения могут быть записаны в виде уравнений равновесия. Применяя метод динамической механики к движущейся материальной точке, необходимо записать ее «равновесное»
состояние под действием заранее заданных сил, объединенных сил реакции, фиктивных сил инерции. = о Где F-результирующая сила данной силы, приложенной к точке массы, R-результирующая сила реакции сцепления, наложенная на точку массы, J — сила инерции точки массы, а абсолютная величина равна произведению массы точки и ее коэффициента ускорения, а противоположное направление ускорения: Y = — mw. В формулировке метода кинетической статики сила инерции называется мнимой. Это пото
му, что этот акцент не относится к этому важному пункту. (На самом деле эта инерционная сила приложена к»ускоряющей» материальной точке и сцеплению, наложенному на эту точку. Если к силам F и R прибавить инерционную силу Y, не приложенную к этой точке, то, естественно, уравнение движения становится своего рода уравнением равновесия. По мере движения массы вдоль кривой сила инерции разлагается на 2 составляющие, соответствующие
касательной、 Нормальное ускорение: сила инерции Y в тангенциальном направлении и сила инерции Jn в нормальном направлении (рис. 151), далее JX используется — мкм Ин = — mwni Джей-МВт = JX у Ин. По модулю Я. = М / W \ Ш-Н. Метод кинетической статики и применение материальных точек к несвободным системам приводит систему уравнений: Форекс + ХВ + Ят = 0、 ФН + рН + ин = 0 Число векторных уравнений будет равно числу массовых точек в системе. Если исследуемый объект является твердым телом,
то необходимо создать уравнение «равновесия» для этого объекта с помощью метода кинетической статики. динамика стопы для каждого из mkwh = Fk 4-Rn、 Они включают в себя заранее заданную силу, комбинированную силу реакции, фиктивную силу инерции. Метод кинетической статики может быть использован для решения прямой задачи динамики несвободных систем точек материи, то есть задач, которые определяются движением неизвестных сил. Однако все эти задачи несколько менее трудоемки в обычном режиме way.
By применяя основное уравнение материала » 1X точка системы, то есть k = 1, 2,.. н. Куда? При решении обратной задачи, то есть задачи, в которой движение определяется заданной силой, использование меча и динамики нецелесообразно. Как упоминалось ранее, кинетический метод был описан в этом документе. Это связано с устоявшимися традициями, которые до сих пор часто используются в различных инженерных дисциплинах. (Кроме того, метод
кинетической статики ошибочно называют «принципом Д’Аламбера», который не объясняется в этой книге.) Метод кинетической статики может быть использован, если он входит в число заданных и неизвестных величин: массы материальной точки, момента инерции твердого геля, скорости и ускорения точки, угловой скорости и ускорения твердого тела, момента силы и усилия. Мы рекомендуем решать задачи с помощью кинетостатического метода в следующем порядке: 1) на рисунке показана установочная сила, приложенная к каждой материальной точке. 2) применить принцип прощения связи и сшить силу реакции связи, наложенной на каждую из критических точек L [системы. 3) Добавьте фиктивную силу инерции материальной точки системы к установочной силе
и силе реакции муфты. 4) Выберите систему координат. 5) для каждого важного пункта системы».Создайте уравнение для»равновесия». 6) после решения составленной системы уравнений определите искомую величину. Проблема 363.In в соответствии с законом нагрузка весом 1 > колеблется с пружиной, подвешенной на потолке* = asinu) f. определите натяжение пружины. Масса пружины игнорируется. Начало оси x, которая расположена вертикально вниз, находится в положении равновесия нагрузки. Решение. 2. Сила, приложенная к грузу-его вес Р и сила упругости пружины, ее выступ
Для решения задачи кинетическим методом необходимо решить 363 задачи. Еще добавить фиктивную силу к нагрузке У= — w. (сила инерции называется мнимой. Реальность не связана с нагрузкой.) Зная закон движения груза x = a sin ut, определим проекцию ускорения на ось l. wx = = — ash * sin w/. таким образом, проекция силы Hiicpsui и J на ось x равна П / п ссыт 4 СП = — з. = — о грехе Вт. А. Г. А.
напишите уравнение «равновесия*» нагрузки в проекции на ось X. Уравнение движения может быть дано формально и формально Так как инерционная сила J приложена к нагрузке, но фактически не действует на нагрузку, то равновесие: П + JX У + Ф / = 0.Из этого уравнения мы можем видеть, что: ГХ = — (П + JX используется). Предполагая, что Jx =■an? Грехи, которые мы получаем: На FX = — я П — ■О ’ 2 грех Ио/). ’g в} Требуемое натяжение пружины T равно силе упругости F по модулю и направлено в противоположную
сторону. [Я Т = — П4-а <о ’ грех(по.£1 Легко определить максимальное и минимальное значения силы т. П И * ’/Макс = ИЖ-;-7 ′ ОМС-П-~~ Так… : п. С. 2 (0 * ^ Т ^ П-ААА£ \ с) Так, в частности, P = 2 кг, a = 2 или o)= 100 se / g1, а −38,8 кг ^ G ^-42,8 для равновесной нагрузки пружины, 7 = 2 кг. Не прибегая к кинетическому закону, это прямая problem. it может быть решена с помощью дифференциальных уравнений движения груза в проекции на ось v. Из последнего
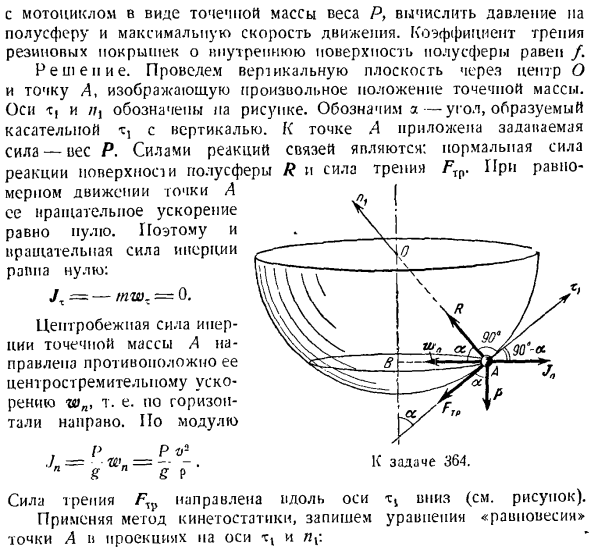
уравнения, учитывая соотношение x-a l, легко найти Форекс = — [п-т-п-ду б \ п о \ е Поэтому использование динамической динамики в этой задаче достаточно трудоемко(необходимо дополнительно определить и изобразить силу инерции) и не имеет преимуществ перед использованием дифференциальных уравнений движения значимых точек. Задача 364.При выполнении цирковых аттракционов мотоциклист движется с постоянной скоростью v по внутренней поверхности полусферы с радиусом R. нарисуйте круг с радиусом LI =
p в горизонтальной плоскости. Эскиз мотоциклиста Если соединение наложено на ускоренную материальную точку, которая не свободна, и ускоряющая точка также действует, то сила инерции приложена к»ускоряющей» точке, частично к соединению. Как известно из статики, систему сил можно свести к паре сил с вектором силы, равным основному вектору, и моментом вектора-торриоса, равным основному моменту. Уменьшение силы инерции дает следующие результаты (меньше, чем в / 2). при постановке кинетического статического метода объясняется, что сила инерции приложена к условно «ускоренным» твердым телам): а) при поступательном движении твердого тела сила инерции уменьшается до результата, который прикладывается к центру тяжести твердого тела.
Абсолютное значение результата равно произведению массы твердого тела на ускорение любой точки и направлено в противоположную сторону от этого ускорения. R (f> = = — Mw (рис. 147); Рисунок 147. Рассчитайте давление и максимальную скорость полусфер с помощью мотоцикла в виде точечной массы массой P. коэффициент трения резиновой шины о внутреннюю поверхность полусферы равен/. Решение. Нарисуйте вертикальную плоскость через
центр O и точку A и нарисуйте произвольное положение точечной массы. Оси M и//показаны на рисунке. a-обозначает угол, образованный касательной m1 и вертикальной линией. Указанная сила прилагается к точке A. R веса. Сила реакции сцепления — это сила реакции R и сила трения F ^на нормальной поверхности hemisphere. At точка A p [Se ускорение вращения V равномерное движение Равняется пуле. Следовательно, и тогда. \ 1__ Вращательная сила инерции^ —-〜
Равный нулю: = — МВт. = 0. Голы: 364 Центробежная инерционная сила точечной массы а направлена в противоположную сторону от ее центростремительного ускорения (wn), то есть горизонтально вправо. По модулю 。 Р П./ Вт= -〜 «Г п г п п」 Сила трения F ^направлена вниз вдоль оси (см. Рисунок). Опишите уравнение равновесияточки А в проекции на ось и ПУ с помощью метода кинетической статики. FT-p » +Лsin a = 0、 -Р-р грех-вы потому что
=0.фотоэлектричество〜 Jn = — и это описывает эту систему О П Уравнения вида: — /Я-п потому что-я — ^ зта = 0、 Ф Р — Так и есть Р-р ЗША — — — потому что а =0.Ф Р Когда вы решаете систему уравнений, она выглядит так: } И-ЖЛ 1 а к-грех / Сова * к Из треугольника ОЛЬВ, cosa=〜, то есть грех л /? ^^ 7 и TGA = Когда вы назначаете эти значения, вы в конечном итоге получаете: , rn, x = / / ex * ±и> 2 Идеальное вертикальное давление, приложенное
к внутренней поверхности полусферы, равно по величине вертикальной реактивной силе R и направлено в противоположную сторону. Четыре Центробежная сила Yn, используемая для решения задачи методом кинетической статики, фактически не применяется к точке A. ускорение Поэтому при решении этой задачи с помощью основных законов динамики необходимо учитывать только те силы, которые естественным образом приложены к массе, то есть P, R и FTp. в проекции mwn = P—R — ’rF™\axis px можно видеть: мзн потому что = р-п грех, — мзн грех= -/: ™топор-
если M =-9 = Ф™Х = о.、 ëP Решением этой системы уравнений является неизвестная величина R и Решение задачи кинетико-статическим методом является несколько громоздким, так как необходимо дополнительно определить и изобразить инерционную силу Jn. Поэтому удобнее решать задачу, используя основные законы динамики. Проблема 365.Ведущее звено сцепленного 4-звена 0 \ 0iAB OX качается вокруг горизонтальной оси Oy, которая перпендикулярна плоскости механизма, согласно закону 9 = cf0sin&F. OxB-04L=/, 0.0.2 = / * L если вес P от силы инерции звена AB, то соединение.4 и B для
определения дополнительного давления. Звено АВ считалось тонким однородным стержнем. Решение. Гипотеза 0 {0 ^ =ВА и оув-о ^ а а,4-линковый пик 0\0 * Ab является a parallelogram. As в результате VA-link имеет фиксированную link0] 0b т. е. И параллельно всегда движется. Прогрессивное движение. При поступательном движении твердог
Mw и прикладывается к центру gravity. In поступательное движение твердого тела, ускорение всех его точек равно вектору. Поэтому достаточно определить ускорение любой точки стержня A B. найти ускорение точки B, которая также является концом звена B. Ж «= Ж » — Ж-ЗП в герцах- По модулю Ускорение Wb образуется связью O, B и углом a = arctg^.Поскольку мы знаем угол поворота звена 0 \ B поскольку это 0 sin, это соответствует времени f = 0.Если подставить/ = 0 в уравнение(3)、 Эти дополнительные давления направлены
вертикально вниз. Проблема 366.Под действием пары сил момента t однородный круговой диск массой P и радиусом r вращается вокруг неподвижной вертикальной оси z, перпендикулярной плоскости. Проекция угловой скорости диска на ось Z равна ш = а/.Где a-константа. Центроид диска с удален от оси вращения на расстояние OS = I. Для AO = h \ \ Oft-7H определите динамическую реактивную силу, 50 футов и величину крутящего момента упорного подшипника A. игнорируйте сопротивление движению. Решение.
Обозначим движущиеся координатные оси, связанные с вращающимся диском. ось Z ориентирована вдоль оси вращения, ось Y Вдоль линии, соединяющей точку O и центр тяжести c диска, ось x вместе с осью y и осью 2 образует правильную систему координатных осей. Заданная сила представляет собой пару сил притяжения диска P и крутящего момента t. поддержите динамическую составляющую силы — J реакция показана в # Ah} # Ay, Raz> Rbx> Pfiy решил задачу методом статики движения. Чтобы
составить уравнение «равновесия» диска, нужно прибавить силу инерции диска к заданной силе и силу реакции связи. Эти инерционные силы Голы 366 Силы, равные основному вектору, и моменты объединяются в пару сил, равных основному моменту. Центр тяжести диска как уменьшение центра инерции, составляющая основного вектора V [nJ \ V [J)\ mc]силы инерции-указывает на главный момент силы инерции на оси через центр
тяжести C, который перпендикулярен плоскости диска. Увеличивает ускорение центра тяжести диска до WQ pa centripetric wcn и вращающихся компонентов wcx. = — Потому что это Mwa, V (nJ)= — MwCn> V (J)= — MwCx Ви? = ВФ = КТМ» = п — в *. В <«= в = MwCl = Дж-г агг. О, да. 。Это был отличный опыт. когда co ^ = af, это выглядит так:= = Таким образом, к центру тяжести диска с, направленному вдоль оси вращения от оси вращения, добавляется сила, равная центробежной составляющей основного вектора силы инерции диска (V y y),
а проекция на ось задается формулой =(О Сила, равная вращательной составляющей основного вектора Инерция диска, которая также добавляется к центру тяжести c диска, является противоположным направлением ускорения вращения wcz точки C, то есть параллельным положительному направлению оси x и ее проекции на ось X. в [Дж = | (2) Основной момент инерции диска относительно оси через центр тяжести диска с перпендикулярен его плоскости. ТФ— ’ СГГ- РГ- ex = x, так что、 = а. (3) Знак главного момента инерции / hp противоположен знаку проекции углового ускорения r2. Согласно методу кинетической статики, он переходит
к составлению»равновесных» уравнений диска в случае наличия определенных сил, сил реакции связей и мнимых сил инерции. Вам нужно создать 6 уравнений равновесия. 2Ф>,= Ракс + Rllx + Вий)= 0、 Г] МХ(ФН)= — па-Дж-РА ВХ-RBy 2Н = 0,£М (П) = — RAxh-я-рН> 2Н = 0, 2 т (п)= м-Джей-eti1 * — В [К) = 0. Здесь значение Vi/’, V \ J \ m [C(1)、(2)、(3)и еще
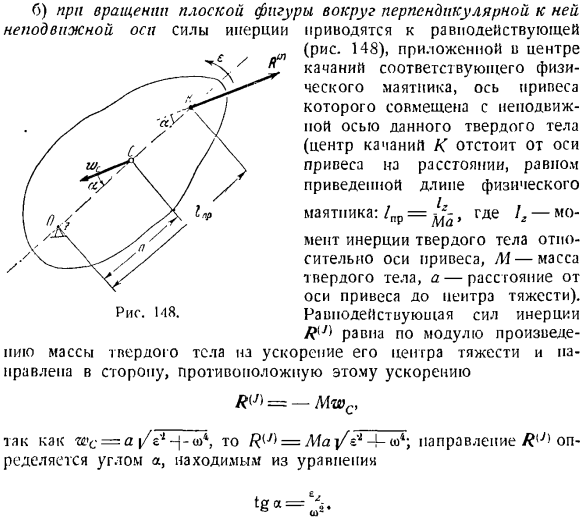
б) при вертикальном повороте плоскости В результате возникает фиксированная осевая инерционная сила е (рис. 148), установленный в центре __ G4 ^соответствующие физические колебания ^ ^ Ось маятника В сочетании с чем-то без движения гг \ Джей поет твердый оси /(y / (центр качели K отстоит от оси Усиление на расстоянии, равном / / > / to / / / сокращение физической длины / / \ / / / О /? / Y ^маятник: / pr=, где\ 2 — \ Yn ^ / me,, T ineRiii твердотельное otio- n ^ ^ ^ x ^ /относительно оси усиления M-масса Твердое тело, а-расстояние от оси усиления до центра тяжести).Рига С8.Результат инерции
Абсолютная величина равна произведению массы твердого тела или ускорения его центра тяжести, которое направлено в противоположную сторону к этому ускорению Поскольку Wc = a [/zl — / — u> 4, R ^ = Ma j / V1-i4; направление R (J) выше определяется углом a, найденным из уравнения. Как видно из полученных результатов, только составляющая опорной реакции упорного подшипника раз не зависит от состояния диска. То есть он не меняется как в состоянии покоя, так и во время вращения
диска. За счет снижения инерции диска в этой задаче можно было выбрать любую точку диска, как центр снижения. Так… С точкой O в качестве центра уменьшения, сила Vn]и и /прикладываются к точке O без изменения величины и направления. ключевые моменты инерции на оси z Изменение размера: когда E = A, вы можете увидеть следующее: =(Р * + 2es) есть. В этом случае первые 5 уравнений остаются неизменными, а 6-е принимает вид: £МЗ(Ф»)
= М + моя = 0. Я Когда вы решаете это уравнение, оно выглядит так: Это будет соответствовать результатам, полученным ранее. Если в этом вопросе необходимо только определить величину крутящего момента, то гораздо проще это сделать, составив дифференциальное уравнение вращения диска вокруг неподвижной оси r. н Ви? = 2 Е7.」 k = I С £тр(К)= М, 1р = 1С + П-А2 = | (г ’+ 2а’) fe-I 6 5 y-е уравнение принимает вид | (Т * + 2a1) ч = М. Итак, 6-е уравнение системы, составленное при решении этой задачи методом кинетической статики, по существу является дифференциальным уравнением для вращения твердого тела вокруг неподвижной оси. Проблема
367.Равномерные круглые колеса с массой P и радиусом r катятся, не скользя по горизонтальным рельсам. Определите момент силы, который необходимо приложить к колесу, чтобы центр тяжести c колеса двигался со скоростью vc = at. Где a-константа. Если коэффициент трения качения равен / k, проверьте также нормальную силу резания рельса R и размер модуля силы трения колеса Frp вокруг рельса. Решение. Установленное усилие прикладывается к колесу: вес колеса и сила удара желаемого момента t. реактивная сила сцепления выводится в направлении нормальной реактивной силы R рельса,
перемещения PA расстояние / центр тяжести c колеса k, а сила трения F ^направление вдоль движущегося направления рельса. Точка С, как полюс, для придания плоскости движения добавляет силу инерции колеса, сила инерции равна основному вектору V <7>силы, а момент равен суть ТК’ \ Сила инерции V добавляется к центру тяжести колеса C, ускорения которого направлены в противоположную сторону от wa, т. е. влево, равную произведению массы колеса
и ускорения его центроида C, то есть V ^ J) = — Mwc. Выберите систему на фиксированной оси с координатами xy, показанными на рисунке. dvCx В гипотезах, ВК-X = в, тогда расширением WCX = = А. я(о Знак главного момента силы инерции колеса M] противоположен знаку проекции углового ускорения er на ось zt. — .= — /CTR С WCX находился в И затем… а)пра ^ = —2Д- Решите задачу с помощью метоторической и статической механики. Если учесть, что все заранее заданные силы, силы комбинированной реакции и силы инерции находятся
в 1 плоскости, то составим 3 уравнения»равновесия». I1F » x = FrfJrV¥= 0、 2; Пятьдесят = Р-Р = О.、 С МС (ФК)= м + — FTpr-РФВ = 0 (3) Используйте выражения (I) и (2) для описания системы (3) в виде. (4 )) РГА т. = о- Если решить систему уравнений «равновесия» (4), то получим: П-Р = 0、 Эта задача также может быть решена с помощью дифференциальных уравнений плоского движения твердого тела. ССХ = £КХ) Мыр = в Fiyt / с?= Дж] МС (Feky k = 1 k = \ k = I Действительно, на рисунке pse, помимо основного вектора и основного момента сил инерции колес, описываются силы и моменты、 Мосе = Р-Р、 Конечно. = т- ’ в-РУ И я думаю, что •* WCX находился на группы PG2 Р XC = WCx = a ’VC =°> <Г= *г= — = >» и Мы
получаем: = п. Р-На ’ О = Р-Р、 Ргл Н〜- Эта система одновременных уравнений совпадает с системой одновременных уравнений(4). Решение задачи методом кинетической статики оказалось более сложным, так как необходимо было определить основной вектор и главный момент виртуальной инерционной силы колеса. Применение дифференциальных уравнений плоского движения твердых тел короче и естественнее, чем использование кинетического статического метода. Задача 368.Нагрузка A и B соединены в печи напитка non-expandable которая поручена через блок D. понижая нагрузку A 1 ″ веса
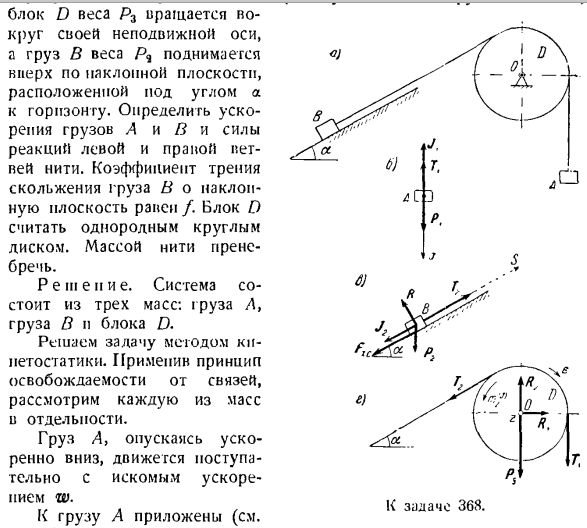
Блок D веса P3 вращается вокруг своей неподвижной оси, а груз B веса Pch поднимается вверх по наклонной плоскости угла a относительно горизонтальной плоскости. Определите ускорение грузов а и В, а также силы реакции левой и правой ветвей нити. Коэффициент трения скольжения груза B вокруг наклонной плоскости равен/.Блок D считается однородным круговым диском. Масса нити игнорируется. Р е ч е н и Е. система состоит из 3-х масс груза L, груза B N блока D. Задача решается методом кинетической статики. Рассмотрим
каждую массу индивидуально, применяя принцип освобождения от отношений. Груз а быстро спускается вниз и движется вперед с требуемым ускорением W. Прикрепленный к грузу а(см. Диаграмма о): 1 набор силы- Его вес равен P1,а сила реакции правой ветви нити равна 7.Ускорение груза Вниз, поэтому результатом его инерционной силы является пауза Вверх: Jx = — L-w, или проекция на ось x: &
Р ГХ Дж \ х = — Д Ш x- Напишите уравнение «равновесия» нагрузки и проецируйте его на вертикальную ось X. Груз B, поднимаясь по наклонной плоскости, движется постепенно с тем же ускорением W. Нагрузка B прикладывается со следующими силами: 1 установленная сила-ее вес P. In случай нормальной силы реакции P наклонной плоскости, силы трения скольжения FTm от нагрузки на наклонную плоскость B, силы реакции левой ветви резьбы T (см. Рисунок C). Ускорение w груза B направлено вверх по наклонной плоскости. Таким образом, комбинированная сила инерции груза в/ 9 направлена вниз параллельно линии максимального наклона
наклонной плоскости. В J2 = — — — ш. его проекции: Джей = — * ВК(указывает направление с-оси figpapa рисунок c). В проекции на ось s создайте «сбалансированное» уравнение для нагрузки. Т2-Пи ЗША -/; Т. С + А * =0.п J ^ = — s ws, FT> c = fN = / P9 cos a, запишите это О Уравнения и формы Т ^ — П9 ЗША — / Р9 потому что — ^ * только WS =0.(2) Если вы выберете центр тяжести твердого тела C в качестве центра замедления, сила инерции будет уменьшена до силы, равной основному вектору. Пары векторов и сил с моментами, равными
основному моменту mc. Основной вектор инерционных сил V свойства-0, п Ти-Пи ЗША — / Р9 потому что — — — * а » 5 = 0、 7-1 T_G) Когда вы определяете неизвестные wx, 7″ и 7’lf из этого уравнения: Р, — Р3 (грех г• — / потерь J)] −8 (5) в Значение 2pt-Ф-2шт — { -/’ > _ 2PtP. Т(1 4-грех 4• / потому что) T_2P, п. (1-ф-грех 4 — / коза) — па | р {- п., (грех + / потому что г)| Если P-Pa (sin a-j — ^ / cos a) wx> 0, то есть ускорение нагрузки A направлено вниз. Если вы решите эту задачу и проигнорируете массу блока D по сравнению с массой товаров A и B
, то, учитывая Ря = 0, вы увидите следующее: g _ Р.11 + Сина + Ф коза) — — — — — — — — — — — П | п.(грех ИИ / Коза в) + ^ Поэтому силы реакции левой и правой ветвей нити, проходящей через блок, различны при рассмотрении массы блока и одинаковы при игнорировании массы блока. В этой задаче, когда необходимо определить давление блока O на ось, при учете равновесия блока (см. Рисунок D), помимо уравнения моментов относительно оси z, необходимо определить давление блока O на ось.、
Также уравнение проекции всех сил на горизонтальную и вертикальную оси: Ри-Т Международный, потому что-Х = 0, — Р2-Т1-Т и грех = о、 Из КРУ. Ри = Т \ соѕ а = ц-ц потому что, К,= + ’А + 7″ зта = Н3-+ А. грех Подставляя значения формул (5) в 7’j и 7 ′ a, получаем компонент силы реакции оси блока и значение R. искомая составляющая давления блока на ось имеет противоположное направление к соответствующей компоненте сил реакции оси Rx и^ и является модульной. Если вам нужно определить только ускорение w нагрузки a>ω в задаче дня, то гораздо проще получить результат, применив уравнение общей динамики (см. задачу 390 ниже) или
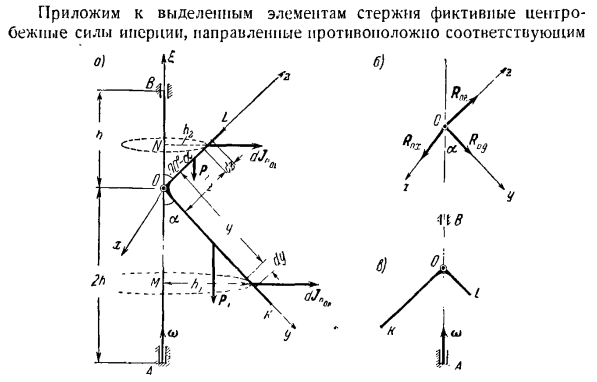
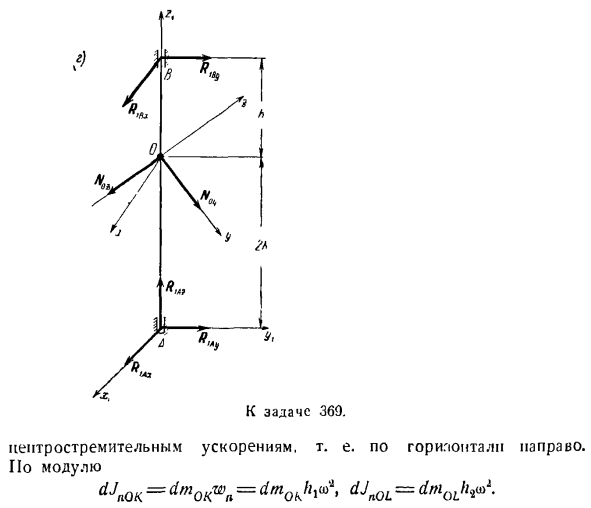
уравнение Лагранжа типа 2. Задача 369.Рыхлый однородный стержень кол изогнут под прямым углом, острым концом прикреплен к вертикальной оси АВ в точке О. найти величину постоянной угловой скорости о>вращения вала. Хорошо сторона стержня отклоняется только на угол а от вертикали(см. рисунок а).Реактивная сила соединения О и опорная реактивная сила упорного
подшипника A и подшипника B также определяются(если все в порядке).a, 01 = b, OA = l2H, 0/3 = h. 7-Длина единицы массы стержня; Решение. Соедините подвижную ось обруча с изогнутым стержнем и валом. 1 (Используйте начало координат шарнира O. укажите ось y вдоль 11 и OL соответственно. рисует ось x, чтобы сформировать декартову систему координат на оси y и оси Z. Координаты мультиплексора. Вес части стержня OK травмирован=вес части
стержня OL равен/ =- В дополнение к заранее установленным силам Px и Pb, сила реакции соединения также должна быть представлена. Коль стержней, присоединиться к совместной. Покажем составляющую силы реакции sharpra O: R0 dmQL = 7 ДЗ、 Применить к выбранным элементам стержневого манекена Значения dmOK и dm0L в формуле (I), а также h,= y sin t. и если присвоить h4 = z cos a, то получим: dJnQK = 7 ^ uso9 грех тьфы,= до 4 потому что ДЗ. (2) Угловая скорость, обусловленная вращением вала, постоянна, поэтому сила инерции вращения выбранного
элемента равна нулю. Мысленно применяя мнимую центробежную инерционную силу, соответствующую каждому элементу стержня кол, составим 6 уравнений «равновесия» для стержня кол. 2 > fky по = R0y + Plcosz-т-р <коша + \ dJnQK грех-Ф (ЛАДНО) + 5 dJnOLSlna: = 0> (Пр)%ФК * = R0z-п я * Ина-П Срна + \ диджей ^ потому что + (ЛАДНО) + \ dJnOL C0S * = ’ (OL) ^ МХ(ФК)=-П т2sin а-Р9 значение COS а + + S * JnOK \ 0M \ — \ dJn0l / ON / = 0, yuk) Ион Присвойте системе уравнение «равновесия»: OM = y w $ a、 ON = Z sin a,= P2 = ^ gb и значения уравнений (2) dJn0K и dJn0L. что получить: R0x = O、 а б R0y — {—да
потому что а-j-ФГБ потому что а-F -?Sin2 СО2 и DY-(- ear9 грех потому что ^ здз = Qт Около 0 а б R0z-да грех — ^ ГБ греха, а-j — ^ В2 грех потому что ^ г ды-\ — cos2 ял а ^ з ДЗ = 0、 Около 0 — грех-потому что ТСО ’ 2 грех потому что \ Ил ды-1о б −7 <Джу * грех потому что ^ zidz = 0、 При выборе точки O, которая находится на неподвижной оси за пределами центра редукции, сила инерции уменьшается до силы, равной основному вектору V [J)>, и момент становится парой сил, равных основному моменту m) K, но V () = — Mwc, и в главном моменте вместо L. = — Здесь, lQ = / c-Ma1.Если центр тяжести С находится на оси вращения плоской фигуры, то основным вектором силы инерции становится пуля, и поэтому система сил инерции сводится к парам. Момент t [o = — / » yy в) по мере движения
плоской фигуры сила инерции уменьшается до силы, равной основному вектору V {J. Рисунок 150. Центр сокращения, и момент Иначе говоря R0v 4-18-го, потому что а-F — ^ ГБ потому что это — грех ’ 1 а + — грех ведь = 0、 R0z—\ га ЗША-ДГ£ > грех-Ф-грех, потому что а-J-А * а = 0、 Вар. ГБ〜, о> * ал. 。 — грех-потому что г — — — грех, потому что это-грех, потому что а = у Когда вы решаете эту систему уравнений, она выглядит так: а л8 грех * 4-Б-потому что ——- 2 (’Г1-sinccosa ’ г. л. Г / Я«.сек, 3(а * грех 4 — потому что СГ) 21 «О,= 0.„О,=-ТГ£|.(А + а) потому что + Т(aa_.Т“) коза И. Ф. Это хорошая вещь. 3(а ’ грех 2 4 — б * я Р0,=
Тан (а + б) СЛН в 4 „(я, А) “ Ж- поскольку to2> 0, вращение стержня KOL, описанного в проблемном состоянии, возможно только для a> b. для A — > b стержень находится в положении, показанном на рисунке. с. Переходите к определению силы реакции упорных подшипников A и B(см. Рисунок D).Давление 7Vf>прикладывается к шарниру О со стороны стержня KOL. Модули, а именно Nоx = -= » о= — Ко、
Поясним новую систему перемещения осей xxy \ Zxt, которая также соединена со штангой и поддоном. Начало координат выбирается в упорном подшипнике A, а ось zx направлена параллельно оси x вдоль оси вала AB, оси оси jc. оси выпускался вместе с осями ЖЖ и ZX, обращается, чтобы сформировать правильную систему координат. Указанная сила NQv и nqz (N0x = 0) и составляющая силы реакции упорного подшипника A и подшипника B: R приложены к валу A B. Х«)= 2л COS в * — ’2ч грех -’ ш * = Когда вы решаете эту систему уравнений, она выглядит так: = 1 Жо * потому что-N0i грех), RiAy = — (НКС потому что-NQy .. \ ,,.. _. 3(л * грех-Джей-Б-потому что а)
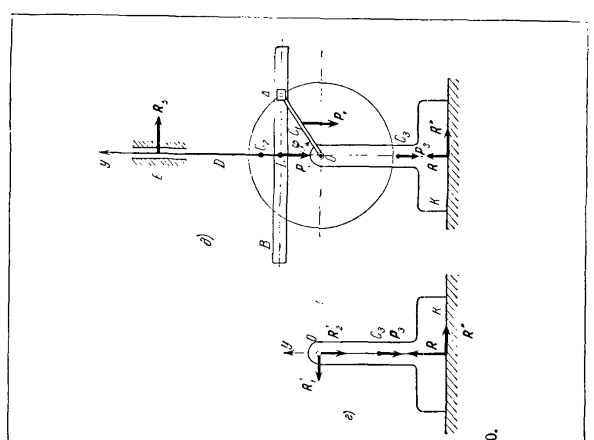
2 O. V = w | («+B) C0S * + 4 (a ’-b’) cos a | • .Т [/Я Ф \ * 3 {или порожка — я-б * я) 3 я ч0,= ты [(*+б) грех т(а, _y Дж、 Тогда, наконец, найти: Н _n _0 П 1 потому что а)’ ИД * — tKiBx—4-ши, а потому что ’ ^ „МФИ. Фау-2 (<р <-* 3) грех ведь не “ Задача 370.Используйте крыло, показанное на рисунке 1, для перемещения вибрационной машины. а. кривошип кулисы ОА с массой Р и длиной r имеет постоянную угловую скорость(0. В первый момент кривошип занял верхнее вертикальное положение. Вес рамки B бортовой рамки и вала D P. 2. если это так, определите вертикальную составляющую вертикального давления
машины на основание и давление оси O коленчатого вала. Вес рамы K равен Pl. Игнорируйте все остальные массы машины. Решение. Исследуемая система состоит из 3 масс кривошипов, закулисной рамы и отцов. Используя метод кинетической статики, мы рассматриваем движения каждой из 3-х масс индивидуально. 1 к кривошипу ОА прикладывается заранее заданная сила-его вес P. На кривошип накладывается следующее звено: ось кривошипа О и рамка сцены Б. Б-это сила реакции оси О \ и/?2, 2 компонента, реактивная сила R frame backstage рамки и Чтобы применить
кинетический метод, необходимо добавить силу инерции кривошипа OL. Vij) равен основному вектору силы инерции, где центр тяжести C / A точка ползучести при уменьшении центра инерции = — Mwc. Скорость вращения Так как кривошип постоянен, то ускорение е = 0 и точка с (центростремительная: Виу〜ЖНК、 Итак, основной вектор силы инерции кривошипа (VlJ) направлен вдоль кривошипа от оси O, а абсолютное значение равно VyJ)=—J w » 2.Основной момент силы инерции равен нулю: m ©= — / sg = 0(или позже) = 0). в результате система сил инерции сводится к результирующей силе, равной V(J).
Направьте ось Y вертикально вверх с осью O коленчатого вала OA в качестве начала координат. В соответствии с кинетическим законом уравнения * rzv-новесия ’ создают кривошип с проекцией на ось Y. — Пт + Ри-т ри + В (К) с COS <Р = V (является J * = — w, а угол поворота кривошипа при равномерном вращении
, получаем следующее уравнение: R = Pt-f P9 + Pe-GSH3 COSCOU Ри = п+ па-п% ChlPt потому что АРФ. Требуемое вертикальное давление направлено в противоположную сторону, где модуль упругости равен реакции R и^. Решение этой задачи кинетическим методом достаточно трудоемко. Такие задачи удобнее решать с помощью теоремы о движении центра инерции материальной точечной системы. Поэтому для определения силы реакции R необходимо учитывать всю систему в целом. account. In в этом случае
реактивная сила равна R3 и внутренняя сила И это не входит в соответствующее уравнение. напишите теорему о движении центра инерции материальной точечной системы в проекции на ось Y. Туалет =£Кг К-1 Внешняя сила, составляющая реактивную силу, составляет 5 сил, 3 силы тяжести Р2, Ре.
Ось, проходящая через центр редукции перпендикулярно фиксированной плоскости. Поэтому при использовании твердого тела необходимо выбрать центр тяжести и уменьшить центр инерции、 В ^ = — MWC в < > = — / СV Уменьшение силы инерции до силы, равной основному вектору, и пары сил, моменты которых равны основному моменту, является одним из ключевых шагов в решении динамики несвободных материальных точечных систем при применении
метода статики движения или уравнений общей динамики(см.§ 5 ниже).Также при определении динамического давления на ось вращающегося твердого тела (см.§ 3 ниже).Отметим, что формальный метод решения задачи связан с силами инерции. Все перечисленные ниже проблемы могут быть решены несколько легко без использования инерции forces. In в этом документе мы опишем, как решить задачу с помощью сил инерции. Это связано с тем, что эти методы все еще очень распространены в инженерной практике из-за широкого исторического tradition. In динамика, проблема колышка, которая не может быть решена без использования инерции force. In в дальнейшем неоднократно проводились сравнения методов
решения задач при использовании и не использовании сил инерции. Основной вектор и основной момент инерции, условно приложенные к ускоренному твердому телу, должны определяться по приведенной выше формуле в зависимости от вида движения твердого тела (поступательное движение, вращение вокруг неподвижной оси, плоское движение).Если вы не можете вычислить главный вектор и главный момент по готовой формуле, а масса распределена непрерывно, то необходимо рассчитать силу инерции выбранного
конкретный Интеграл в пределах соответствующего предела. Реакция направляющей стержня (см. Рисунок е).Что взять: =-/>!-/>、-/>、1-я、 Откуда R = Pi — \ — P,+ P,+ MyCt(4) Осталось определить МУС: МУС = ПУ \ Ф-mqy2 + / £ 3″(5) Где yy y *и uz-координаты центроида масс C, C2 и C3.С Дж /,= Г, потому что уу = Р соз (МАФ УЗ = — ОС3 = const и、 И затем… Дж / | =-СО2, потому что г * = — rw2 в кос(О, Джей?3 = 0、 Формула (5) принимает вид: Мой c =—(Pt + 2 /Щcos a> f. (6) Подставляя выражение (6) в выражение (4), получаем: Р = ДЧ + / в + пр — ^(Пи + 2cos <Ф. Когда вы удаляете весь системный кадр и применяете
теорему снова к движению центра инерции проекции на ось y, R2 находится. В последнее время в инженерной практике метод кинетической статики постепенно вытесняется применением основных законов динамики и общих теорем. В следующем разделе мы рассмотрим, как уменьшить силу инерции массы твердого геля, вращающегося вокруг неподвижной оси. Задача 358.5 определяет главный момент инерции [gpc]для колеса 3 точки B планетарной передачи, показанной на фиг. а. Колесо 1 находится в неподвижном состоянии. Радиус колеса/и 3 равен. Передача приводится в движение кривошипом OLV, который вращается вокруг оси O, перпендикулярной плоскости, в которой расположен механизм, с постоянной угловой скоростью w0.Какова сила инерции колеса 3? Решение. Первичный момент инерции колеса 3 Для точки в определяется по следующей формуле: Кривошип вращается равномерно, а колесо коробки передач круглое. Поэтому угловая скорость всех колес не изменяется со временем.
Смотрите также:
Предмет теоретическая механика

