Оглавление:





Метод источников и стоков
Метод источника и приемника. Этот метод гидромеханики позволяет Рикину сначала обратиться к пространственной задаче обтекания тела, заменив обтекаемое тело такой системой источников и стоков, чтобы поверхность тела функционировала как 1 ток в этом случае, очевидно, алгебраическая сумма богатого источника, вводимого в границы тела, должна быть равна нулю, чтобы построить желаемую схему течения. В зависимости от заданной формы поверхности обтекаемого объекта, очень сложно выбрать систему вышеупомянутых источников и приемников.
Во многих простых случаях рассматривается обратная задача нахождения формы поверхности, которая может быть получена за пределами границ обтекаемого тела с заранее заданной центровкой источника.
- а) равномерно распределенные источник и Сток вошли в равномерный прямой поток.
Если предположить, что скорость равномерного потока направлена вдоль оси, то источник диффузии мы помещаем в точку на оси, а сток-в точку на той же оси. Полученный поток для осесимметричного течения становится осесимметричным, и в соответствии с принципом суперпозиции потенциал потока выражается формулой.
Здесь для построения радиус-вектора текущей поверхности, оттянутой от стока, угол, образованный с осью радиус-вектором r, который оттягивается в определенной точке p в поле от источника, равен. Людмила Фирмаль
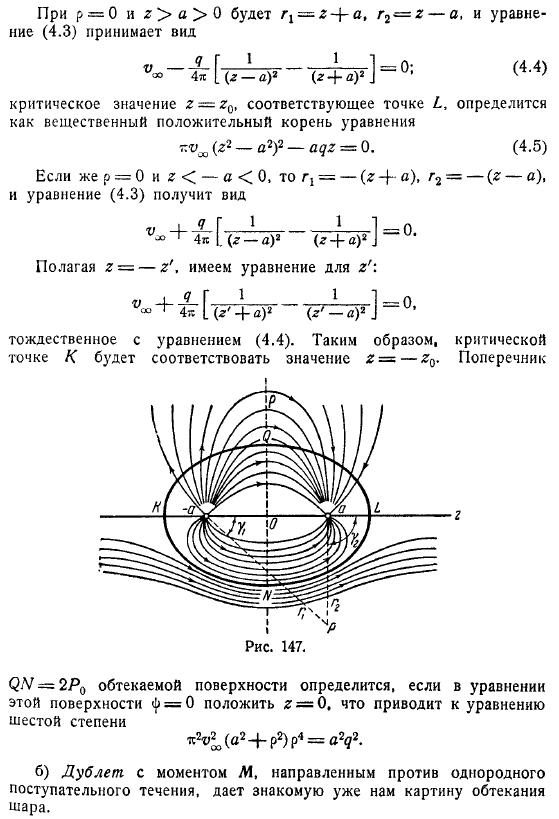
Вы можете применить графический метод для добавления хорошо известных скалярных полей из Максвелла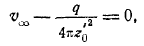 , как описано в предыдущей главе. Текущая поверхность состоит из внешнего сегмента оси og и замкнутой поверхности, полученной вращением эллипса вокруг оси.
, как описано в предыдущей главе. Текущая поверхность состоит из внешнего сегмента оси og и замкнутой поверхности, полученной вращением эллипса вокруг оси.
Критический удар Точка, в которой поток расходится и скорость исчезает, определяется условиями Или Предположим, что мы имеем следующее уравнение То же, что и уравнение. Таким образом, критическая точка k соответствует значению. Диаметр Если мы включим уравнение этой поверхности, то будет определена обтекаемая поверхность, которая является уравнением 6-го порядка
- б) дублет с моментами, направленными к постоянному прямому потоку, обеспечивает знакомый вид потока вокруг шара.
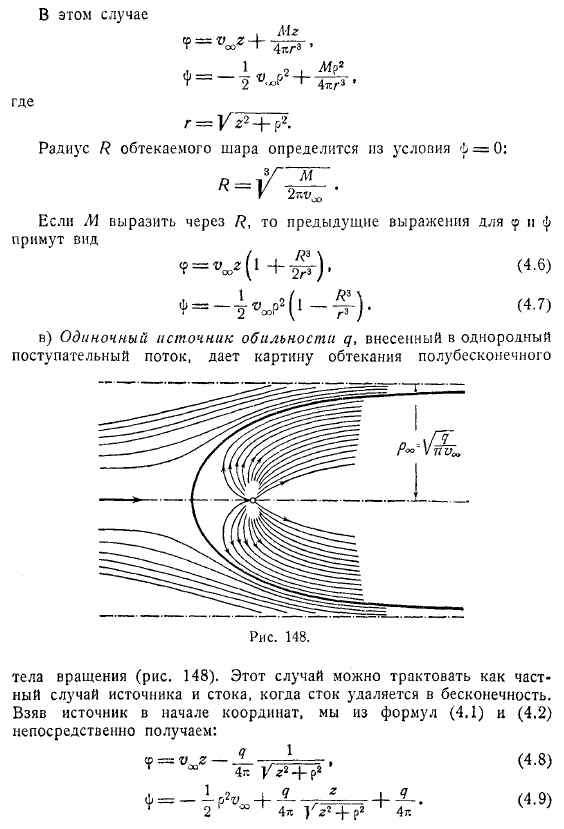
Куда? В этом деле Мг. Радиус обтекаемого шара i определяется из условия Если l1 представлен обтеканием осесимметричных тел , то предыдущее выражение имеет следующий вид в) один источник обильного q, введенный в равномерный поступательный поток, обеспечивает диаграмму течения вокруг полубесконечного Этот случай можно интерпретировать как частный случай источника и стока, когда Сток движется в бесконечность.
Если вы получаете источник в начале координат, вы можете получить его непосредственно из выражения. Форма поверхности обтекаемого полубесконечного тела определяется уравнением Критические точки определяются по следующим критериям.
Из этого делаем вывод, но используя предыдущее уравнение, получаем следующий вид: Формула выглядит следующим образом. Людмила Фирмаль
Это означает, что при увеличении r поверхность обтекаемого тела приближается к цилиндру асимптотически. г) обилие переменных на элементах из источников, линейно распределенных по сегментам оси Он вводится в однородный поток трансляции и создает потенциальный поток.
- И текущие функции Если алгебраическая сумма обилий линейно распределенных источников света равна нулю, то последний Интеграл исчезает, и текущая поверхность состоит из отрезка оси и замкнутой поверхности Накройте сегменты с источником и сливом.
Если, наоборот, установить внешний вид поверхности. Поскольку p является известной функцией r, он ищет неизвестное распределение источника и приемника в определенных сегментах оси. Там, где эта поверхность обтекает ток, она сводится к решению интегрального уравнения.

