Оглавление:
Метод интегрирования по частям
Пусть 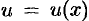 и
и 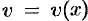 — функции, имеющие непрерывные производные. Тогда
— функции, имеющие непрерывные производные. Тогда 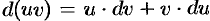 . Интегрируя это равенство, получим
. Интегрируя это равенство, получим
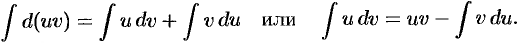
Полученная формула называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла 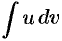 к вычислению интеграла
к вычислению интеграла 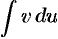 , который может оказаться существенно более простым, чем исходный.
, который может оказаться существенно более простым, чем исходный.
Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей 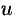 и
и 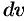 (это, как правило, можно осуществить несколькими способами); затем, после нахождения
(это, как правило, можно осуществить несколькими способами); затем, после нахождения 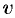 и
и 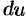 , используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.
, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.
Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
- Интегралы вида
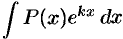 ,
, 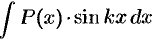 ,
, 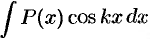 , где
, где 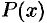 — многочлен,
— многочлен, 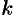 — число. Удобно положить
— число. Удобно положить 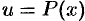 , а за
, а за 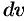 обозначить все остальные сомножители.
обозначить все остальные сомножители. - Интегралы вида
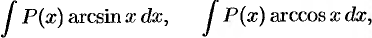
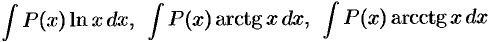 . Удобно положить
. Удобно положить 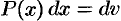 , а за
, а за 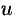 обозначить остальные сомножители.
обозначить остальные сомножители. - Интегралы вида
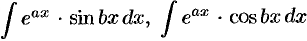 , где
, где 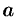 и
и 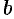 — числа. За
— числа. За 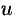 можно принять функцию
можно принять функцию 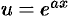 .
.
Пример №30.6.
Найти 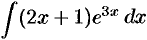 .
.
Решение:
Пусть 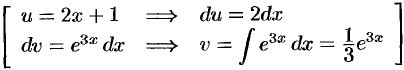 (можно положить
(можно положить 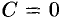 ). Следовательно, по формуле интегрирования по частям:
). Следовательно, по формуле интегрирования по частям:
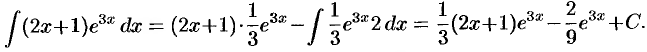
Пример №30.7.
Найти 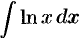 .
.
Решение:
Пусть 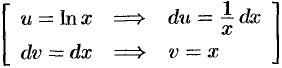 . Поэтому
. Поэтому
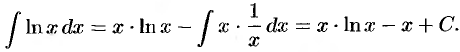
Дополнительные примеры:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Метод непосредственного интегрирования |
| Метод интегрирования подстановкой |
| Понятия о рациональных функциях |
| Дробно-рациональная функция |

