Интегрирование некоторых сложных функций — метод, основанный на использовании техники интегрирования некоторых сложных функций и формулы Ньютона-Лейбница.
Для нахождения определённых интегралов от некоторых сложных функций можно использовать следующий алгоритм:
I. Найдите неопределённый интеграл от заданной функции, используя формулу
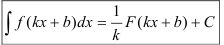
(если возникают сложности, перечитайте методические указания к выполнению задания 20).
Для получившейся первообразной вместо слагаемого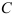 
запишите вертикальную черту с верхними и нижними границами интегрирования.
По формуле Ньютона-Лейбница в первообразную вместо переменной подставьте сначала верхнюю границу, затем знак «минус», затем нижнюю границу интегрирования.
Советуем рассмотреть реализацию данного метода на примере:
Пример решения заказа контрольной работы №70.
Вычислите
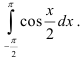
Решение:
Сначала найдем неопределенный интеграл от заданной функции как интеграл от некоторой сложной функции, введя границы интегрирования:
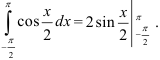
Подставим сначала верхнюю, потом нижнюю границы интегрирования:
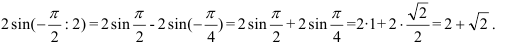
Ответ:
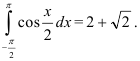
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
