Пусть необходимо найти корень уравнения вида 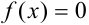 с точностью
с точностью 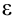 , если известно, что корень принадлежит промежутку
, если известно, что корень принадлежит промежутку 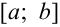 . Графически это означает, что необходимо найти нули
. Графически это означает, что необходимо найти нули
функции — значения переменной 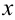 , в которых график пересекает ось
, в которых график пересекает ось  , и эти значения по условию должны принадлежать промежутку
, и эти значения по условию должны принадлежать промежутку 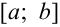 .
.
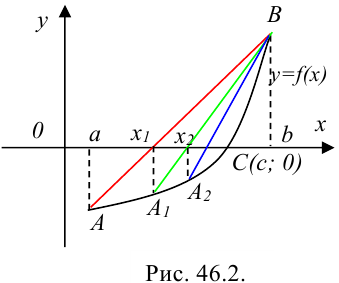
Рассмотрим функцию 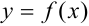 на отрезке
на отрезке 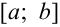 (рис. 46.2). График данной функции обязательно пересекает ось
(рис. 46.2). График данной функции обязательно пересекает ось 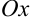 в некоторой точке
в некоторой точке 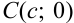 . Наша задача — найти абсциссу этой точки — значение
. Наша задача — найти абсциссу этой точки — значение 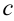 .
.
Выполним следующие действия:
- Проведем хорду
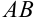 . Она пересекает ось
. Она пересекает ось 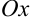 в точке с абсциссой
в точке с абсциссой 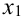 .
. - Выберем точку на кривой, абсцисса которой равна
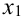 — точка
— точка 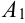 .
. - Проведем хорду
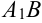 . Она пересекает ось
. Она пересекает ось 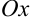 в точке с абсциссой
в точке с абсциссой 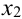 .
. - Выберем точку на кривой, абсцисса которой равна
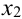 — точка
— точка 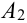 и т.д.
и т.д.
Будем продолжать этот процесс до тех пор, пока разность между последующим 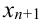 и предыдущим
и предыдущим 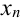 значениями переменной
значениями переменной 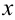 не станет меньше заданной в условии задачи точности
не станет меньше заданной в условии задачи точности 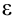 , т.е.
, т.е. 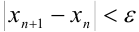 . Это означает, что
. Это означает, что 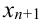 ,
, 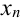 практически не будут отличаться от
практически не будут отличаться от 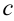 .
.
Выведем формулы для нахождения 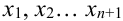 :
:
1. Выпишем координаты точек 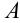 и
и 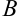 :
: 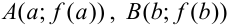 .
.
2. Составим уравнение прямой 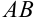 :
: 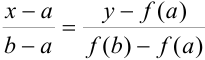 .
.
3. Найдем точку пересечения прямой 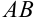 с осью
с осью 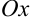 . Она имеет координаты
. Она имеет координаты 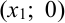 . Заменим в уравнении
. Заменим в уравнении 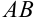
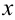 на
на 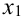 ,
, 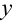 на 0:
на 0: 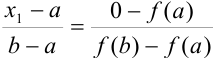 .
.
Выразим 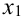 . По свойству пропорции
. По свойству пропорции 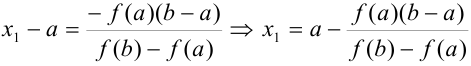 .
.
4. Поскольку для нахождения 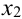 нужно проводить новую прямую через точки
нужно проводить новую прямую через точки 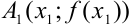 и
и 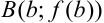 и находить точку ее пересечения с осью
и находить точку ее пересечения с осью 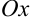 , произведем по аналогии следующую замену: роль
, произведем по аналогии следующую замену: роль 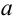 будет выполнять
будет выполнять 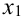 , роль
, роль 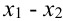 . Получим, что
. Получим, что 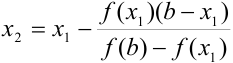 .
.
5. Обобщим проведенные рассуждения. Для нахождения 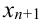 будем использовать следующую формулу:
будем использовать следующую формулу: 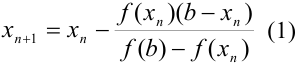 .
.
В рассмотренном нами случае при проводимых преобразованиях точка 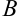 оставалась неподвижной.
оставалась неподвижной.
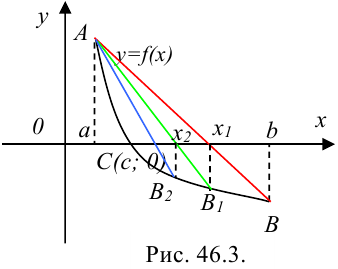
Возможен и другой вариант: неподвижной может быть точка 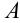 (рис. 46.3). В этом случае будем использовать другую формулу:
(рис. 46.3). В этом случае будем использовать другую формулу: 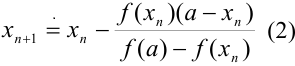 .
.
Для удобства формулы (1) и (2) можно объединить в одну: 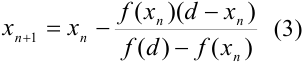 , где
, где 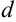 — абсцисса неподвижной
— абсцисса неподвижной
точки (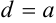 или
или 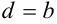 ),
), 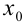 — конец отрезка
— конец отрезка 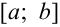 , не являющийся абсциссой неподвижной точки,
, не являющийся абсциссой неподвижной точки, 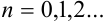
Правило выбора неподвижной точки:
Неподвижной точкой является тот конец отрезка 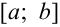 , для которого знак функции в этой точке совпадает со знаком второй производной функции в той же точке.
, для которого знак функции в этой точке совпадает со знаком второй производной функции в той же точке.
Пример №46.2.
Найти приближенное решение уравнения 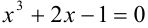 на
на 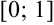 , использую метод хорд с точностью
, использую метод хорд с точностью 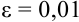 .
.
Решение:
Составим функцию 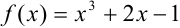 .
.
1. Выберем неподвижную точку. Для этого найдем 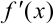 и
и 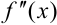 :
:
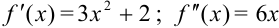 . Найдем знак функции и второй производной на каждом конце отрезка: в точках 0 и 1.
. Найдем знак функции и второй производной на каждом конце отрезка: в точках 0 и 1.
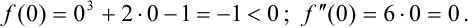
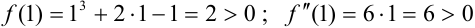 . Видим, что при
. Видим, что при 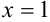 знак функции совпадает со знаком второй производной. Следовательно,
знак функции совпадает со знаком второй производной. Следовательно, 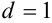 — абсцисса неподвижной точки.
— абсцисса неподвижной точки.
2. Поскольку при решении задачи расчеты получаются достаточно громоздкие, их удобно выполнять с использованием компьютера, например, программы Microsoft Excel.
В качестве шапки таблицы можно предложить следующий вариант:

В столбце 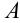 будет указываться номер выполняемого шага
будет указываться номер выполняемого шага 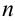 . Первое значение
. Первое значение 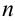 всегда выбираем равным 0.
всегда выбираем равным 0.
В столбце 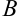 будут располагаться значения
будут располагаться значения 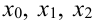 и т.д. В качестве
и т.д. В качестве 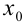 в ячейку
в ячейку 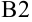 занесем значение того конца отрезка, который не является абсциссой неподвижной точки. В нашем случае это
занесем значение того конца отрезка, который не является абсциссой неподвижной точки. В нашем случае это 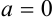 .
.
В столбце 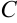 будут содержаться значения функции в точках
будут содержаться значения функции в точках 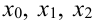 и т.д., необходимые для расчета
и т.д., необходимые для расчета 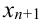 по формуле (3). Для нахождения
по формуле (3). Для нахождения 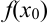 в ячейку
в ячейку 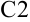 введем формулу. Поскольку
введем формулу. Поскольку 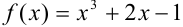 , а первое значение
, а первое значение 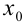 находится в ячейке
находится в ячейке 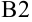 , то формула будет иметь вид:
, то формула будет иметь вид: 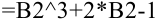 .
.
В столбце 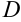 будет осуществляться проверка того, не превосходит ли
будет осуществляться проверка того, не превосходит ли 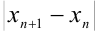 заданной точности
заданной точности 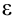 . Эта проверка будет начинаться с
. Эта проверка будет начинаться с 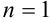 , и ячейка
, и ячейка 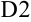 не заполняется.
не заполняется.
Столбцы 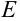 и
и 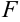 — вспомогательные. Поскольку в формуле (3) используется
— вспомогательные. Поскольку в формуле (3) используется 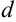 и
и 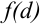 , то их можно один раз записать соответственно в ячейках
, то их можно один раз записать соответственно в ячейках 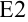 и
и 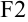 и в дальнейшем делать на них абсолютные ссылки.
и в дальнейшем делать на них абсолютные ссылки.
После заполнения второй строки, она будет иметь вид:

Начнем заполнение третьей строки. Номер шага в ячейке 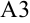 будет равен 1.
будет равен 1.
Для расчета 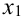 в ячейке
в ячейке 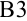 применим формулу (3), которая в программе Microsoft Excel примет вид:
применим формулу (3), которая в программе Microsoft Excel примет вид: 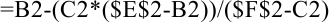 . Ссылки на ячейки
. Ссылки на ячейки 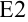 и
и  содержат знак
содержат знак 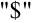 , т.е. являются абсолютными, и при копировании данной формулы меняться нс будут.
, т.е. являются абсолютными, и при копировании данной формулы меняться нс будут.
Для расчета 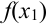 в ячейке
в ячейке 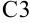 достаточно просто скопировать формулу из ячейки
достаточно просто скопировать формулу из ячейки 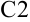 , и она будет иметь вид:
, и она будет иметь вид: 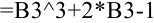 .
.
В ячейку 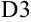 занесем формулу для расчета модуля разности между последующим и предыдущим значением
занесем формулу для расчета модуля разности между последующим и предыдущим значением 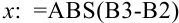 . Произведем проверку: если содержимое этой ячейки больше
. Произведем проверку: если содержимое этой ячейки больше 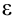 , то расчеты необходимо продолжить, меньше — закончить.
, то расчеты необходимо продолжить, меньше — закончить.
После заполнения третьей строки, она будет иметь вид:
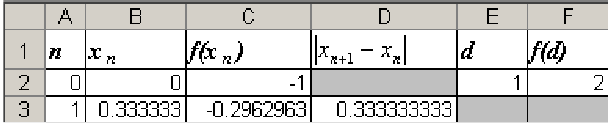
Достоинства программы Microsoft Excel с том, что нам достаточно ввести только формулы, все расчеты машина произведет сама. Видим, что содержимое ячейки 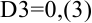 больше заданной точности
больше заданной точности 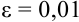 , следовательно, расчеты следует продолжить.
, следовательно, расчеты следует продолжить.
Все основные формулы уже введены, в дальнейшем будем использовать только возможности автозаполнения. После выполнения следующих шагов таблица будет иметь вид:
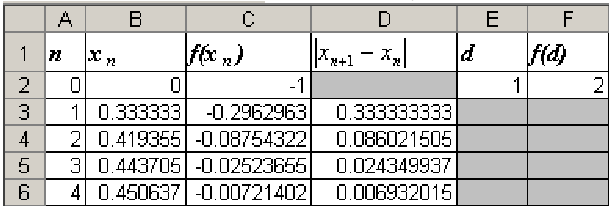
Видим, что в ячейке 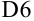 содержимое 0,006932015 стало меньше заданной точности
содержимое 0,006932015 стало меньше заданной точности 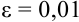 , следовательно, расчеты следует закончить и в качестве приближенного решения уравнения взять
, следовательно, расчеты следует закончить и в качестве приближенного решения уравнения взять
последнее 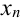 с точностью 2 знака после запятой. В нашем примере это
с точностью 2 знака после запятой. В нашем примере это 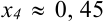 .
.
Ответ: 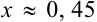 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Погрешности вычислений с приближенными данными. |
| Понятие алгебраического и трансцендентного уравнения и методов их приближенного решения. |
| Метод касательных. |
| Задача численного интегрирования. |

