Оглавление:


Метод хорд
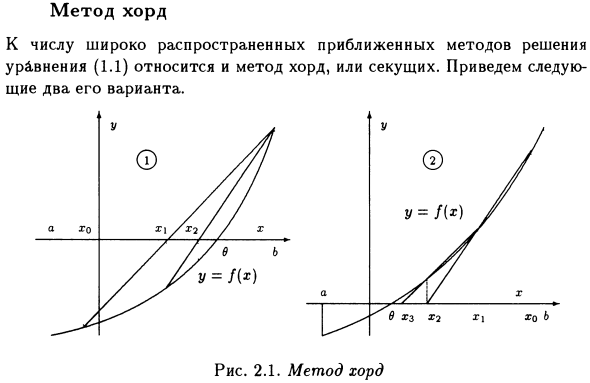
Метод хорд. Общие методы приближения для решения уравнения (1.1) включают аккордовые или секущие методы. Есть два варианта: Рисунок 2.1. Метод хорд 1.
- Одно начальное значение. Одна начальная точка x0 произвольно выбирается вблизи искомого решения (то есть из интервала [a, 6]), после чего
все последующие точки определяются последовательно. Людмила Фирмаль
Предположим, что значение xn известно (читатель может принять n = 0). Далее, xn + i определяется как пересечение линии, проходящей через точки (xn, f (xn)) и (6, / (6)) с осью x (см. Рисунок 2.1).
Уравнение этой прямой на плоскости (x, y) можно описать в виде V ~ Dxn) f (b) -f (xn) xxnbxn, поэтому для абсциссы пересечения ^ n + 1- xn J \ xn). B-xn f (b) -f (xn) (2.5)
- Однако это также означает, что существуют уравнения в виде (2.6) двух начальных значений, если они находятся на рассмотрении. На этот раз произвольно выбирают два числовых значения Xq и Xj. Затем определите X2 из них и постройте xs … и т. Д. По xp X2. Как именно?
Предположим, вы уже построили аппроксимации до xn. Далее, следующее значение xn + 1 берется как пересечение линии, проходящей через точки (xn-b / (^ n-1)) и (* n »f (xn)) с осью x (рисунок 2.1).
В этом случае читатель снова предполагает, например, что n = 1. Людмила Фирмаль
Форма уравнения для этой линии на плоскости (x, y) имеет вид y- / (ln-1) _f (xn) — / (Jn- l), чтобы получить абсциссу желаемого пересечения (xn + i, 0), просто подумайте: если y = 0, то x = xn + i: xn-1f (Xn) xnf (xn-l) f (xn) -f (xn-l) (2.7)
Во втором выражении 2.7) Γn (r) = x- / (r) / (r) — ( 2.8) является частным случаем рекурсии (1.3a)
Смотрите также:
| Известные методы. | Метод касательных. |
| Метод «вилки». | Начальное приближение. |

