Метод Гаусса является более универсальным, чем правило Крамера, так как позволяет находить решения в следующих случаях:
- Число уравнений не равно числу неизвестных.
- Если в правиле Крамера
.
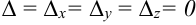Введем следующие понятия:
Матрица 
, составленная из коэффициентов при неизвестных, называется основной матрицей системы.
Матрица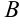 
, состоящая из элементов матрицы и столбца свободных членов, называется расширенной матрицей.
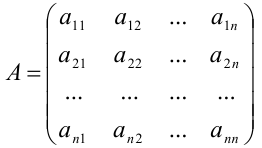
Суть метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы, т.е. приведении основной матрицы системы к треугольному виду, когда под ее главной диагональю стоят нули.
Это достигается с помощью элементарных преобразований матрицы над строками. В результате таких преобразований не нарушается равносильность системы, и она приобретает треугольный вид, т.е. последнее уравнение содержит одну неизвестную, предпоследнее две и т.д. Выражая из последнего уравнения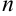 
-ую неизвестную, с помощью обратного хода получают значения всех неизвестных.
Пример №4.2.
Решите систему уравнений методом Гаусса:
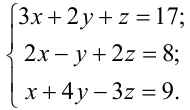
Решение:
Выпишем расширенную матрицу системы и приведем её к треугольному виду: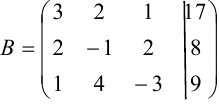 
Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных коэффициентов при последующих вычислениях.
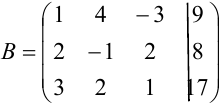
Первую строку полученной матрицы умножаем последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом 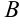будет иметь вид:
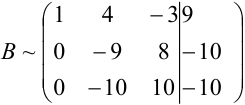
Для упрощения вычислений умножим третью строку на (-0,1) и поменяем ее местами со второй строкой. Тогда получим:
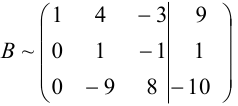
Далее, умножая вторую строку матрицы на 9 и складывая с третьей, окончательно получим:
Восстановим из полученной матрицы систему уравнений равносильную данной, начиная с последнего уравнения:
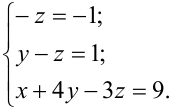
Из последнего уравнения находим: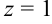 
.
Подставим 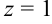во второе уравнение системы: 
; 
.
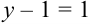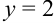После подстановк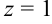и и 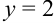в первое уравнение получим: 
; 
; 
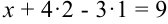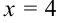. Итак, , , .
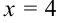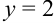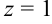Проверка:
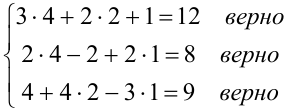
Следовательно, решение системы найдено верно.
Ответ: , , .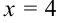
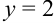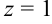Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
