Оглавление:
Метод эквивалентного преобразования электрических цепей
Сущность и цель преобразований
Цель преобразования электрических цепей состоит в упрощении схем путем эквивалентных преобразований, приводящих к уменьшению числа ветвей и узлов. Эквивалентные преобразования входят во все методы расчета в качестве первого шага в последовательностях расчета. Под эквивалентными преобразованиями мы будем понимать преобразования одной части схемы, при которых в остальной части величины токов и напряжений остаются неизменными, как и сама схема.
Расчет цепи при последовательном соединении элементов и закон Ома для ветви, содержащей ЭДС
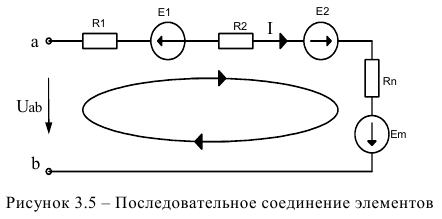
Рассмотрим электрическую цепь при последовательном соединении и ЭДС и резисторов, когда величина тока во всех элементах одинакова.
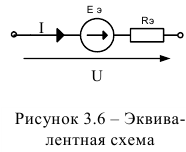
Все величины ЭДС и резисторов известны, как и напряжение на входе цепи. Необходимо упростить цепь до двух элементов (рисунок 3.6) и определить величину тока.
Для решения задачи выберем произвольное направление тока 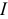 и обхода контура и на основании второго закона Кирхгофа составим уравнение:
и обхода контура и на основании второго закона Кирхгофа составим уравнение:
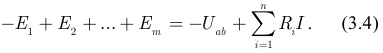
Учитывая, что ток 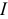 одинаковый во всех резисторах, выносим его за знак суммы и вводим обозначения:
одинаковый во всех резисторах, выносим его за знак суммы и вводим обозначения:
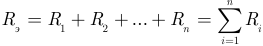 — эквивалентное сопротивление, определяемое в виде арифметической суммы всех последовательно соединенных сопротивлении;
— эквивалентное сопротивление, определяемое в виде арифметической суммы всех последовательно соединенных сопротивлении;
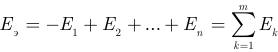 — эквивалентная ЭДС, определяемая как алгебраическая сумма ЭДС.
— эквивалентная ЭДС, определяемая как алгебраическая сумма ЭДС.
С учетом выполненных обозначений, уравнение приобретает вид:

Схема имеет вид (рисунок 3.6), а величина тока:

Расчет цепи при параллельном соединении элементов
Задана электрическая цепь, содержащая параллельно соединенные элементы, т.е. на всех элементах напряжения одинаковые (рисунок 3.7). Величины сопротивлений резисторов заданы 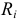 и токи источников тока
и токи источников тока  . Необходимо рассчитать ток
. Необходимо рассчитать ток 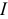 .
.
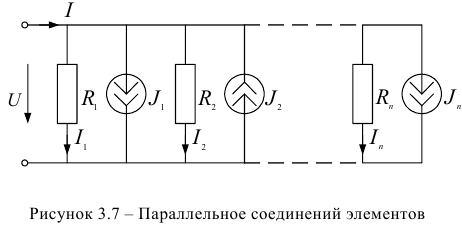
Решение задачи выполним на основании первого закона Кирхгофа, предварительно выбрав направления токов в ветвях, с резисторами от верхнего узла с большим потенциалом к нижнему с меньшим потенциалом:

В представленном уравнении все подтекающие токи взяты со знаком «+», а оттекающие — со знаком «-». Т.к. величина тока в любом резисторе может быть найдена по закону Ома:

то ток  на входе цепи может быть вычислен по выражению:
на входе цепи может быть вычислен по выражению:
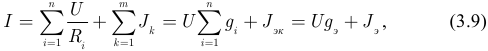
где 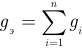 — эквивалентная проводимость всех ветвей с резисторами определяемая как арифметическая сумма проводимостей всех параллельно соединенных резисторов;
— эквивалентная проводимость всех ветвей с резисторами определяемая как арифметическая сумма проводимостей всех параллельно соединенных резисторов; 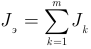 — ток эквивалентного источника тока, определяемый как алгебраическая сумма всех параллельно соединенных источников тока. Знак тока источника тока положителен, если он направлен от узла и отрицателен, если он направлен к узлу.
— ток эквивалентного источника тока, определяемый как алгебраическая сумма всех параллельно соединенных источников тока. Знак тока источника тока положителен, если он направлен от узла и отрицателен, если он направлен к узлу.
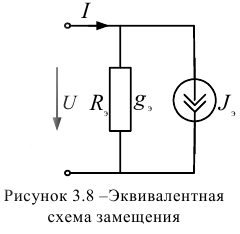
В соответствии с последним уравнением можно зарисовать эквивалентную схему замещения (рисунок 3.8).
Расчет цепи при смешанном соединении элементов
Под смешанным соединением элементов понимают такие соединения, при которых цепь содержит одновременно последовательно соединенные элементы и параллельно соединенные элементы.
Задача 3.1.
Рассчитать эквивалентное сопротивление для схемы, представленной на рисунке 3.9, если:
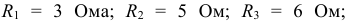
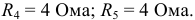
Решение:
На первом этапе объединим последовательно соединенные элементы  и
и 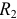 и параллельно соединенные элементы
и параллельно соединенные элементы 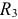 и
и 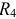 :
: 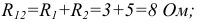
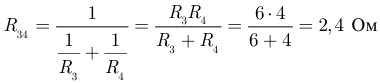
В результате получаем упрощенную схему (рисунок 3.10).
На втором этапе суммируем сопротивления 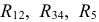 и получаем эквивалентное сопротивление всей схемы относительно входных зажимов 1 и 2:
и получаем эквивалентное сопротивление всей схемы относительно входных зажимов 1 и 2: 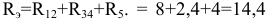 Ом.
Ом.
Задача 3.2.
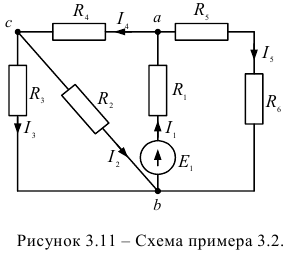
Задана электрическая цепь (рисунок 3.11.). Для величин элементов: 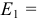
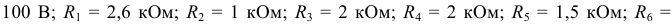
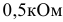 выполнить расчет величин токов в ветвях электрической цепи.
выполнить расчет величин токов в ветвях электрической цепи.
Решение:
Выбираем направления токов в ветвях электрической цепи с учетом направления ЭДС 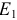 . На первом этапе объединяем резисторы
. На первом этапе объединяем резисторы 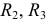 и
и 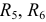 .
.
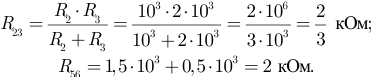
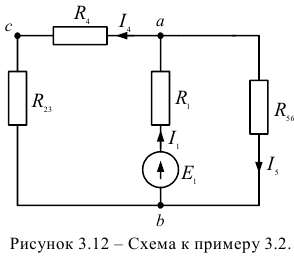
На рисунке 3.12 представлена упрощенная схема. Объединяем сопротивления ветвей, подключенных параллельно, к узлам  и
и  :
:
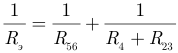
Следовательно:
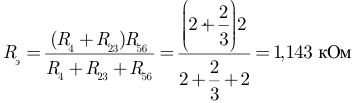
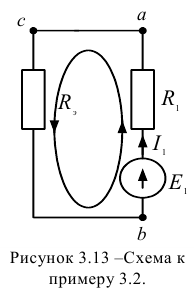
На рисунке 3.13 получена неразветвленная электрическая цепь.
Применяем второй закон Кирхгофа для замкнутого контура:
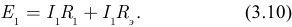
Решаем уравнение относительно тока 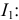
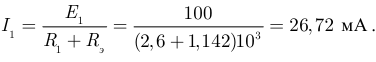
Вычисляем напряжение 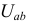 по закону Ома:
по закону Ома:
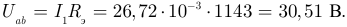
Тогда:
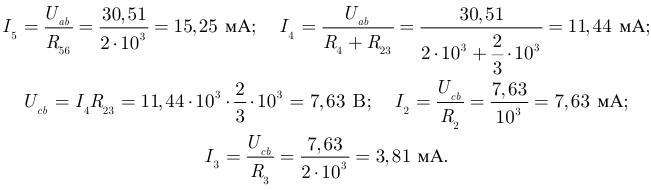
Выполним проверку вычислений по балансу мощностей:
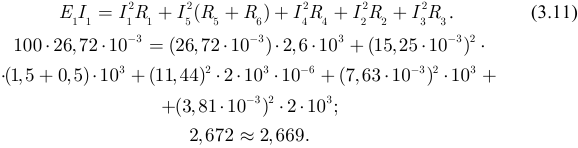
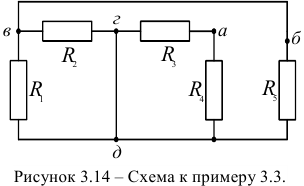
Задача 3.3.
Пользуясь методом преобразования, рассчитать эквивалентное входное сопротивление электрической цепи (рисунок 3.14.) относительно точек 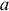 и
и 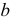 если величины элементов имеют значения:
если величины элементов имеют значения:
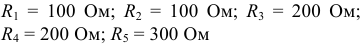
Решение:
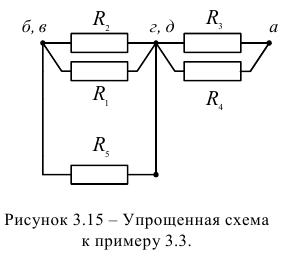
Так как схема содержит ветви без элементов, то узлы и точки с равными потенциалами можно объединить. Объединяем точку в и б и узел г с узлом д. Упрощенная схема представлена на рисунке 3.15. Рассчитаем эквивалентные сопротивления 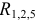 и
и 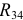 :
:
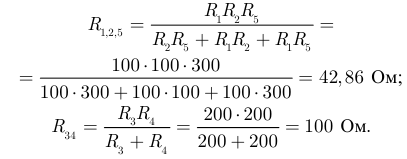
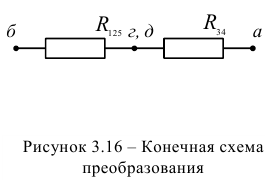
Эквивалентное сопротивление всей цепи относительно точек а и б, в соответствии с новой схемой (рисунок 3.16):
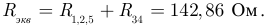
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:

