Оглавление:




Метод эйлера для определения критических сил. вывод формулы эйлера
- Метод Эйлера для решения Это критическая армия. Эйлера Существует несколько методов изучения равновесной устойчивости упругих систем. Основы и технологии применения этих методов изучаются на специальных курсах, посвященных проблемам
устойчивости различных объектов, встречающихся в строительстве и технике. Наиболее универсальным является динамический метод, основанный на исследовании колебаний систем, близких к заданному положению равновесия. Во-первых, его применение требует специальных знаний в области динамики упругой системы, а во-вторых, это основное, что находит отражение
в практике машиностроения. Метод Эйлера основан на анализе ветвей Людмила Фирмаль
возможных равновесных форм упругой системы. Пусть рально сжимается и полностью обдумывает свои мысли о деталях прямого стержня. При низких сжимающих силах прямая линия стержня имеет стабильную форму. Один цент.- Большая сила 461in, превышающая некоторые критические значения, делает его
неустойчивым и имеет устойчивую криволинейную форму. Таким образом, в P>p kr теоретически возможно иметь две формы равновесия. Возникает ветвь формы в состоянии равновесия, минимум сжимающей силы, которая называется критической силой. Таким образом, при критической силе наряду с исходной прямой формой возможны примыкающие, очень близкие к ней
- криволинейные формы. По определению Эйлера, критическая сила-это » сила, необходимая для минимального наклона колонны.»Если вы хотите узнать больше об этом вопросе, обращайтесь:В. Болотин» бессмысленная задача теории упругой устойчивости » (гос. Изд-во физ.Мэтт литературы, 1961). Рассмотрим, что для того, чтобы вывести формулу Эйлера, центр некоторого поперечного сечения поддерживается сжатым стержнем в центре(рис. 390) слегка отклоняется от прямого состояния. Изгибающий момент любого
сечения равна г-н Дифференциальные уравнения изгиба. Придерживайтесь следующего: с?2О м РТ)них~Э~’ Или ^+^=0 , Куда? К Е. Одна * Это будет записано в (15.1) (15.2) Интеграл дифференциального уравнения (15.1) принимает вид V-A coz KX+B zsh KX. ‘(15.3)используйте граничные условия для определения значений любых констант A и B. Первые граничные условия: x=0 и y=0, и-0. Таким образом, формула для криволинейной оси(15.3) имеет вид: (1=81p:. (15.4) таким образом, стержень изгибается в синусоиде. Вторые граничные условия: x-I и V-0, zsh K1=0. 1) B=0;2) 81pk1=
0. История * Знак минус используется, поскольку выбранные оси имеют отрицательную кривизну и положительный момент. 462 в первом Людмила Фирмаль
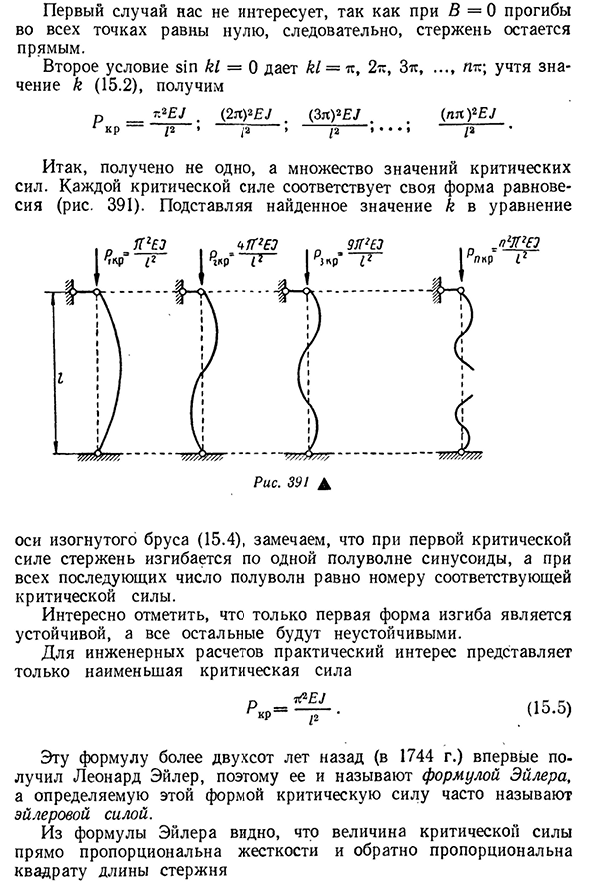
случае b=0 и отклонение всех точек равно нулю, поэтому нас это не интересует, поэтому стержень прямой. Второе условие§1П К1=0 получаем К1=к,2К,ЗК…»Учитывая значение Il; K (15.2)、 1Р КР -. (2л)2е/(зл)2е/. (ЛП) 2Е/ /2’/2Р•• * ÷ * / а Таким образом, получается не одна, а величина многих критических сил. Каждая критическая сила имеет свое собственное состояние равновесия. 391). Присвойте выражению найденное значение K Рис-391А Ось криволинейной балки (15.4) показывает, что при первой критической силе стержни изгибаются полуволнами синусоиды, а при последующих полуволна
х их число равно числу соответствующих критических сил. Интересно отметить, что стабильна только форма первого изгиба, а все остальное неустойчиво. Практический интерес представляет только наименьшая критическая сила для инженерных расчетов 1&E. One 2/2 (15.5) Эта формула была впервые получена Леонардом Эйлером более двухсот лет назад (1744), ее часто называют формулой Эйлера, а критическая сила, определенная в таком виде, называется силой Эйлера. Из Формулы Эйлера, видно, что критическая сила прямо пропорциональна жесткости и обратно пропорциональна
квадрату длины стержня Для стержня, работающего на упругой стадии 463, критическая сила зависит только от геометрических размеров стержня и модуля упругости материала, но от прочностных характеристик материала, из которого изготовлен стержень, например, она не зависит от марки стали. ST. 3, для стали и для высокосортной стали, модуль упругости почти это же, поэтому критическая сила также равна. Два стержня с одинаковыми геометрическими размерами, но выполненные из разных сталей, работают на упругой стадии, теряя устойчивость при одинаковой критической силе. Таким образом, между работой стержня на сжатие и растяжение возникает резкая разница. Предельная сила растяжения напрямую зависит от прочностных характеристик
материала и поэтому различна для разных марок стали, в то время как при сжатии в пределах упругости наблюдается совершенно иная картина. При сжатии он быстро падает с увеличением длины, но конечная сила растяжения не зависит от длины стержня. Продольный изгиб сжатого стержня особенно опасен тем, что происходит внезапно, и поэтому в растянутом стержне, который препятствует в конструкции неправильно распределенным размерам сжатого элемента, признаки опасных состояний часто возникают до выхода из строя, а в сжатом стержне, как правило, не устанавливаются возможные признаки потери устойчивости. При
этом особое внимание уделяется устойчивости сжатого стержня. При выводе формулы Эйлера было обнаружено, что шарнирный стержень на конце изгибается по синусоиде и не может найти численное значение отклонения. (Значение интегральной константы оставалось неопределенным. Это связано с тем, что было использовано приблизительное выражение б/2в (1х2 4 — &2O=0. Если применить строгое дифференциальное уравнение 4 — ^=0, (15.6) В случае R > R cu можно найти прогиб стержня. Интегрирование уравнения(15.6) осуществляется с помощью сложных специальных функций. Изучение этого вопроса выходит за рамки нашего курса
Смотрите также:

