Оглавление:







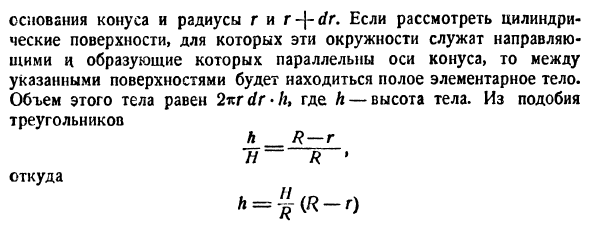

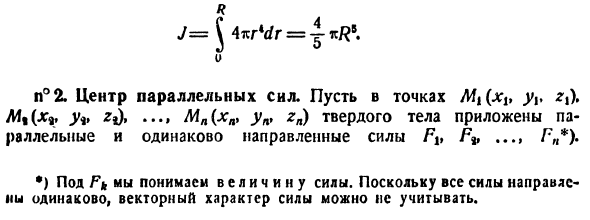



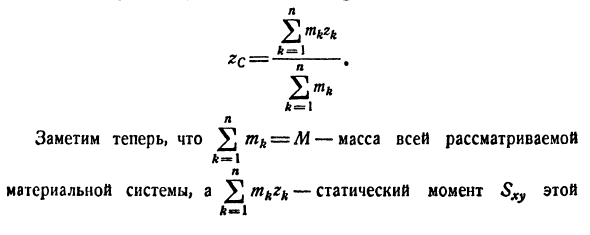









Механические применения определенного интеграла
Механическое применение конкретных интегралов № 1. Статический момент и момент инерции. В механике важную роль играет концепция объекта малых размеров, который рассматривает важную точку, геометрическую точку, но не игнорирует ее массу. Момент инерции материальной точки M относительно точки O (или линии Ox или плоскости xy) является произведением массы m точки M на квадрат расстояния d от точки O (или линии Ox или плоскости xy соответственно) это. Ji = m (P (соответственно, Jx = md \ Jxy = m (P).
- Понятие статического момента S9 точки M (S и Sxy соответственно) относительно O (или Ox или xy) также вводится, где масса m точки M умножается на степень расстояния d. S0 = MD, Sx = MD, Sxy = MD. Но ситуация здесь сложнее. Потому что при рассмотрении некоторых важных точек M, M ‘соответствующее расстояние d, d! Потому что оказывается, что это полезно приписать … Если говорить о S9, если материальная точка находится на оси, г около 1 м 2 / Рисунок 242. Sx * my x * Рисунок 241. я; / Sxy’m Если точка O включена, вышеуказанные символы можно легко ввести. Эта ось должна быть координатой, точка O должна быть началом координат, а d должна быть координатой точки Af (рис. 240).
Однако, если точка M находится в плоскости или пространстве, нет разумной причины из-за этого или расстояния d от точки O.Основание конуса и радиус r и r — * — др. Объем этого тела составляет 2 * г др • ч. Где А — рост. Из сходства треугольников ч _ р-р и ~ р Откуда h = ‘l- (R-r)
Когда эти круги действуют как направляющие, а генератор рассматривает цилиндрическую поверхность, параллельную оси конуса, между этими поверхностями имеется полое тело. Людмила Фирмаль
DV = 2K-G-R (R-R) др. Поскольку расстояние от оси конуса всех точек выбранного простого поля равно r, r3 (/? — r) др. смысл R о Вот еще одно решение той же проблемы: Как мы уже видели, момент инерции относительно центра окружности с радиусом R равен kR *. если Разделите конус на базовые диски, как в предыдущем примере, а затем момент инерции одного диска (толщина dx) Для оси конуса он равен kgKx (поскольку можно предположить, что масса диска равномерно распределена по кругу).
Но мы уже нашли это смысл 3) Найти момент инерции относительно центра шара с радиусом R. Выберите «элемент» шара, находящийся между двумя выходами Сферическая поверхность с радиусами r и r -f- dr. Объем такой Элемент равен сферической области 4itг9 Его толщина др. Расстояние от центра шара для всех точек элемента равно r, поэтому dj = 4itrldr и R J = ^ 4Ttrkdr = jKR \ и № 2. Предположим параллельную центральную точку силы Mt (xlt Y > r,). Af «(jc9, yv Mn (xn ynt zn) твердое тело Параллельная и изотропная сила Fv F% t Fn *). •) Ft означает величину силы. Поскольку все силы направлены в одном и том же направлении, характер вектора сил незначителен.
Нужно найти результат и точку его применения. Сначала сложите силы F \ и />. Из курса физики мы знаем, что результат R параллелен им, ориентирован в одном направлении, равен сумме F, и -f- F ^ относится к точке C. Разделить на Обратно пропорционально силе, то есть MgS ‘_ f \ C’ M, Fx ‘ Найдите уравнение для абсциссы x «Точка C», используя формулу *), которая разбивает сегмент в этой точке. y / g_ | — \ — XjF) X-Ft + F, ‘Y * Здесь, к уже найденному составному элементу R, «третья сила F%.
- Проблема опять в сложении двух сил. Как вы можете видеть, их составной элемент R» параллелен им и направлен в одном направлении. , Всего R ‘+ F% = F -J- F * -f- F3 и относится к точке C. «Разделительный сегмент C» G8 делится на части, обратно пропорциональные силе K’ и F% , (7) Абсцисса х! Согласно пункту «С» это: „At_x» R «-J- x т l- R «+ F> — (Fl + Ft) + Ft Это ~ F. + F. + F, • Если вы добавите здесь силу Fit, вы найдете результат силы Ft, Fi, а также абсциссу его точки приложения. Продолжая это обсуждение, мы заключаем, что система сил параллельна им, ориентирована в одном направлении, равна их сумме и приводит к применению к точке C (xc, yn> * s) *.
(8) Замечания. 1) Как вы знаете, сила, приложенная к телу, передается по линии его действия. Но тогда все *) Для точек, лежащих на плоскости xy, они были угаданы нами. В гл. VIII вы можете видеть, что эти формулы также сохраняются в случае пространства.Точки на этой линии равны, и неясно, почему точка C заслуживает внимания, а ее координаты задаются уравнением (8).
, Мп (возможно, выбрав и изменив последнюю на линии силового воздействия), силы остаются параллельными друг другу и все еще направлены Представь одну сторону. После этого результат изменится, но поскольку направление силы не отражено в уравнении (8), точка C остается в точке приложения. Следовательно, точка С определяется двумя факторами. Это точка, выбранная для величины силы Fk и точки приложения Mh, но она не зависит от направления силы C.
Чтобы ответить на это, поверните все силы Fj, F & Fn в точку приложения MltЛ14 Людмила Фирмаль
В этом отношении точка C называется центром параллельной силы Fk (но ее необходимо добавить: для выбранной точки в приложении). Отказываясь от предположения, что точка AfltМ4Мп взята на том же теле и рассматривается как произвольная точка в пространстве, мы не можем говорить о передаче силы Fk вдоль линии действия, но название называется формулой «центра параллельной силы». Точка C, заданная в (8), сохраняется. 2) Особенно, когда все точки находятся в одной плоскости, точка C также находится в той же плоскости. Если эта плоскость фактически берется в плоскости xy, zt = z% = … = zn = Ot, (8 ) Для Zq = 0. № 3. Центр тяжести.
Рассмотрим систему с n вещественными точками Ml (xv yv Zi), M% (Xp yif Zg), Mn (xn, Yn, Zn), масса mi% mt, mn. Эти точечные веса представляют собой систему сил, которые параллельны и равномерно направлены. Центр С этих сил называется точечным центром тяжести Afj, M%, …> Mn. Координаты точки C задаются уравнением (8). Где Фу означает вес точки Mk. Однако вес точки Mk связан с ее массой mk соотношением Fk = t & м Где £ = 9,81 — i — ускорение, сообщаемое телу под действием силы тяжести, св-сек. Это падает очень близко к поверхности земли.
Подставляя Fk = mkg и треть уравнения (8) и уменьшая g,N ZC n- • 1 N Обратите внимание, что = M — общая масса N Материальная система, и £ tkkk — это статический момент Система для плоскости XY. так * С М * Это координата Zq центра тяжести в пространственном распределении массы.
Если масса распределена в плоскости xy, второй аналогичный аргумент, применяемый в уравнении (8), имеет вид (U) Из уравнений (9) и (10) Sxy = Mz0 Sx = My0 (U) Это *) а) Статический момент пространственной материальной системы не изменяется ни в одной плоскости, если вся масса системы сосредоточена в ее центре тяжести. б) Если общая масса системы сконцентрирована в ее центре тяжести, статический момент плоской материальной системы относительно оси в плоскости системы не изменится. Используя предельный переход, уравнения (9) и (10) и, следовательно, (11) расширяются в случае непрерывного распределения массы.
Применять установленные общие результаты в особых случаях. I. Центр тяжести плоской кривой. Для однородной плоской кривой с n ° 1 и плотностью 1, б Sx = \ yds. но Поскольку масса кривой равна ее длине M = s, уравнение (10) становится б США = \ ^ ярдов но Пример. Найти ординату центра тяжести полукруга **) y = VR * -x \ (12) •) Ведь любой самолет можно принять за лежачий самолет. Точно так же для плоских материальных систем любая ось в плоскости системы может быть принята как Odg. **) Понятно, что * £ = 0 по соображениям симметрии.
В этом случае s = nR и [по уравнению (2)] SX = 2R \, следовательно = 0,637 /? Интересно сравнить уравнение (12) с уравнением (19) в §3. Это дает представление о площади поверхности, образованной вращением кривой y = f (x) ^> 0 вокруг оси Ox. Форма уравнения (19) имеет вид L = 2v \ yds. Так где это было L = s-2ityc. Уравнение (14) Первая теорема Паппа — Гурдин.
Площадь поверхности, образованная вращением плоской кривой вокруг непересекающейся оси, равна длине кривой вращения x пути, пройденного ее центром тяжести. Замечания. 1) Условие, что кривая не пересекает ось вращения, является существенным. Формула для L устанавливается только для f (x)> 0 и требует повышения. 2) Эта теорема была впервые открыта александрийским математиком Папом (III в. До н. Э.). В средние века многие достижения древней науки были утрачены в Европе (в основном сохранились в исламской культуре). В 17 веке эта теорема была заново открыта швейцарским математиком Гулдином.
Суть теоремы состоит в том, что если известны две из трех величин L, yCf, третья величина будет найдена немедленно. (14) Рисунок 249.Поэтому момент Sq не учитывается при размещении показанных точек. Аналогично, момент Sx вводится только в том случае, если точка M находится в плоскости, содержащей ось Ox. В этом случае ось координат Oy, перпендикулярная оси Ox, проведена через O, а d означает координату точки M (рис. 241).
При пространственном расположении материальных точек момент Sx вокруг оси не учитывается. Наоборот, момент Sxy в этом случае вводится очень естественно, когда он означает координату z точки M>, отсчитываемой вдоль оси Oz, перпендикулярной плоскости xy через d (рис. 242).
Пример. 1) Если полукруг вращается вокруг своего диаметра, площадь образованной им сферы составляет L = 4kR *. Кроме того, s =, следовательно, Уравнение (13) получено снова. 2) Поверните тот же полукруг вокруг касательной, параллельной диаметру (Рисунок 249). Где центр тяжести Радиус окружности — следовательно, площадь поверхности вращения L = * /? 2 k (1-A) R = 2 k (k-2) /? » II. Изогнутый трапециевидный центр тяжести.
Если масса равномерно распределена при плотности, равной 1, вдоль трапеции, окруженной линией x = a, x = b, y = 0, y = f (x)> 0, ее статический момент Sx И Sy выражаются как интегралы *) б Sx = ^ y * dxt Sy ^^ xydx. (15) Тем не менее, Трапециевидная масса равна площади F (которая также может быть определена с помощью интегрального расчета). Это позволяет найти центр тяжести трапеции.
Его ордината задается формулой (10) (M заменяется на F), а абсцисса — аналогичной формулой. = (16) Пример. 1) Нашли ли вы ординату центра тяжести полукруга, окруженного осью Ox и полукругом y = \ ZrR? -х \ 1 2 = найдено при a = n ° 1 [ссылка (5)]. смысл Читатель заметит существенное отличие от уравнения (13), которое дает центр тяжести полукруга. 2) Найти центр тяжести фигуры, заключенной в линию * = 0.х-у = 0, у = грех х.*) Выше мы получили первую из этих формул, которые применяют прямоугольное представление статического момента к базовой полосе.
Здесь мы можем дать другой вывод по формуле. Центр тяжести полосы находится в центре. Масса полосы равна площади ydx. Так что dSx ~В]== (для dx) — == уУ (используется тот факт, что статический момент может быть рассчитан путем концентрации массы в центре тяжести).
‘= [sin xdx = 1, $ x = -j jj s \ n * xdx = ~ 9о0 К / 2 Sy = V x sin xdx = 1. смысл Сравнить выражения б а Второй — это объем объекта, образованный трапецеидальным вращением вокруг оси Ox. Это очевидно Подставьте это значение Sx в уравнение США = -p-% узнать В CSS == W> Откуда (17) V = F * 2icyc. Это Вторая теорема Паппа-Гурдина. Объем объекта, образованного вращением вокруг оси, которая не пересекает плоскую фигуру, равен площади фигуры, умноженной на траекторию движения центра тяжести. здесь «/ 2 ~ / 2 F =
Условие, что диаграмма не пересекает ось вращения, является существенным. Используется при применении первого выражения (15), полученного для случая y = f (x) ^> 0. Как и первая теорема того же автора, текущая теорема применяется, когда известны три величины V, F и две из двух. Например, если полукруг вращается вокруг своего диаметра, V = jv / A и уравнение (17) дает yc = ^ R. III. Центральный номер телефона. Если объект T однороден и плотность равна 1, его масса равна объему, M = V, уравнение (9)
Например, в случае конуса с n ° 1 и основания на плоскости xy мы обнаружили, что существует [Уравнение (6)]. V— ^ kR ^ H, так То есть центр тяжести конуса находится на его оси *) 1 От основания до высоты. В качестве другого примера, радиус /? Подумайте о полушарии. Предположим, что плоскость диаметра совпадает с плоскостью xy. Если вы выберете базовый диск с радиусом r из полусферы (рис. 250), вы легко найдете его Рисунок 250 dS ^, = (кг9 дз) z = * (R * -r9) z дз. Отсюда R (R * z-r3) dz = j kR *. K = π /? Так из (18)
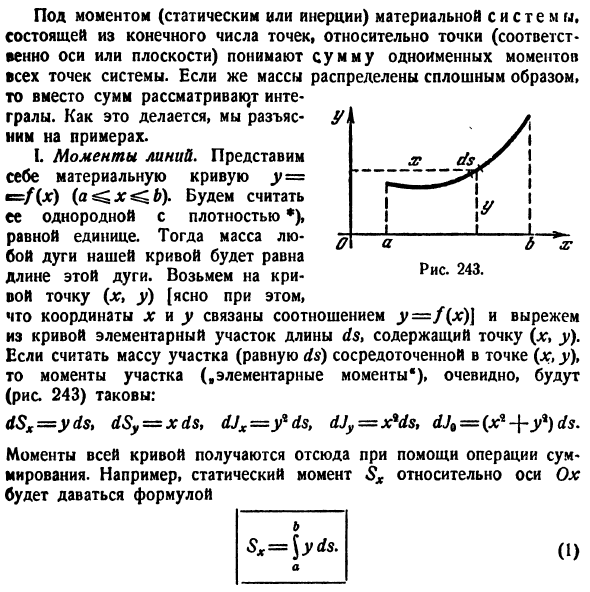
Момент (статический или инерционный) материальной системы, состоящей из конечного числа точек относительно точки (оси или плоскости соответственно), понимается как сумма моментов с одинаковым именем во всех точках системы. Если масса распределена непрерывно, то вместо суммы рассматривается интеграл. Вот пример того, как это делается. I. Момент скандала. Представьте материальную кривую y = e = f (jc) (a ^ x ^ b). Плотность *) считается однородной.
В этом случае масса изогнутой дуги равна длине этой дуги. Возьмите точку (x »y) на кривой [очевидно. Координаты x и y связаны соотношением y — f (x) \, а базовый участок длины ds, содержащий точку (x, y), вырезан из кривой. Учитывая массу графика (равную ds), центрированную в точке (dg, y), момент растяжения (элементный момент *) явно (рис. 243): dSx = yds, dSy = xds, dJx = y * ds, dJy = x9ds, dJQ = (x * — \ — y *) ds Отсюда момент всей кривой получается с помощью операции сложения. Например, статический момент Sx относительно оси Ox задается как Рисунок 243.
Кроме того, y следует заменить на / (x), ds = V ^ l ~ \ -y’x dx, а пределы a и b являются пределами изменения абсциссы x. В качестве примера найдите полукруг $ x y = Yf? -x * (- R ^ x ^ R). Поэтому, где = R J = (2) •) Если масса распределена вдоль кривой, плотность означает отношение массы дуги к ее длине.
I. Момент плоского человека. В этой группе примеров мы предполагаем, что масса равномерно распределена по конкретной плоской фигуре и что плотность (то есть отношение массы фигуры к ее площади) равна 1. 1) Найдите прямоугольные моменты Sa и Ja с основанием a и высотой h относительно основания. Решения. Выберите базовую полосу (рис. 244) из прямоугольника.
Основная полоса имеет ширину dz на расстоянии z от основания. Масса полосы равна ее площади a dz, а расстояние от всех ее точек до основания равно z. так Отсюда Это Sa = J az dz, Ja = Jazgdz, dSa = az dz, dJa = az9 dz. (3) 2) Найти момент инерции J0 окружности радиуса R относительно центра O. Решения. Выберите основное кольцо, содержащееся между кругом с радиусом r и r- * dr из круга.
(Рисунок 245). Так как площадь кольца составляет 2 кг др, и все его точки удалены от O на расстояние r, дДжа = 2 кг2 др Откуда R J = 2k J r3 dr = ^. Рисунок 245. 3) Изогнутая трапеция окружена линиями с x = a, x = b, y = 0, y = f (x)> 0. Найти моменты Sx, Sy, JJ y *. Решения. На трапеции выберите базовую полосу, параллельную оси Oy, с интервалом x и шириной dx (Рисунок 246).
Поскольку все точки полосы расположены на одинаковом расстоянии от оси Oy (потому что площадь полосы равна ydx) dSy = xy dx, dJy = x * y dx, b b Sy = J jcy s / lg, Jv = J JC2_V rfjc. .g Чтобы найти момент полосы вокруг оси Ox, возьмите полосу в виде прямоугольника. Тогда вы можете использовать уравнение (3). Здесь просто напишите y вместо h и dx вместо a. дать dSx = y y4dx, dJx = y yVjc. Осталось обобщить эти основные моменты. Например Откуда 246 для дх диаграмм. б х (4) В качестве примера найдите полукруг Sx с осью Ox внизу и полукругом вверху. (-R ^ x ^ R). Уравнение (4) является R -R
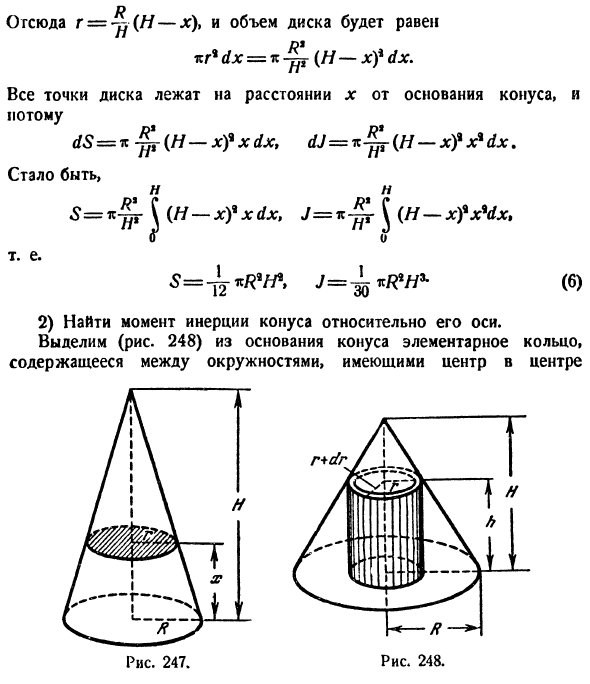
Уравнение (4) является R $ (/? — ^ If * = | [/? * (5) III. Момент телефона. В этой группе примеров рассматриваются материальные тела. Они предполагают, что плотность *) однородна и равна 1. I) Найти статический момент инерции и момент инерции конуса относительно дна. Радиус основания и высота конуса обозначены буквами R и I. Выберите базовый диск в конусе, параллельном основанию, на расстоянии x от основания и толщиной dx (Рисунок 247). Если радиус диска равен r, из подобия треугольника г _ н-х 7? N ‘ • J, где плотность — это отношение веса к объему.
Следовательно, r = jj (H — x), а объем диска равен: dx = K-j ^ (I-xy dx. Поскольку каждая точка на диске находится на расстоянии х от основания конуса, dS == n-jjf (H-x) * xdx, dJ-it-˜- (H-xfx * dx. так N S = * jjr ^ (H — x) * xdx, J = * jjr 5 фW-xfx% dx% J = -w kfN * — Это (6) 2) Найти момент инерции конуса вокруг оси. В нижней части конуса выберите основное кольцо, заключенное между кружками, центрированными в центре (Рисунок 248). Рисунок 247.
Смотрите также:
| Методика применения определенного интеграла к решению практических задач | Приближенное вычисление определенных интегралов |
| Геометрические приложения определенного интеграла | Определители 2-го порядка |

