Механическая система. Классификация сил, действующих на систему
Под механической системой в механике понимается мысленно выделенная совокупность взаимодействующих между собой материальных точек (или тел). Таким образом, положение и движение каждой точки (или тела) системы зависит от положения и движения всех остальных точек.
Система материальных, точек, движение которых не ограничено какими-либо связями и определяется лишь силами, действующими на эти точки, называется системой свободных точек. Примером такой системы может служить солнечная система, все планеты которой можно рассматривать как материальные точки.
Система материальных точек, движение которых ог-раничено наложенными на них геометрическими связями, называется системой несвободных точек. Примером такой системы может служить любой механизм, являющийся всегда системой искусственно соединенных между собой материальных тел (звеньев), совершающих под действием приложенных сил определенное движение.
Действующие па несвободную систему силы можно делить на активные силы и реакции связей. К активным силам, как известно еще из статики, относятся все силы, кроме реакции связей ‘).
При решении задач динамики силы, действующие на систему, часто бывает удобно делить по другому признаку: па силы внутренние и внешние.
Внутренними силами системы называются силы, с которыми действуют друг на друга точки или тела данной системы.
Внутреннюю силу системы будем обозначать в дальнейшем символом 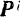 .
.
Внешними силами системы называются силы, с которыми действуют на точки данной системы точки или тела, не входящие в состав этой системы.
Внешнюю силу системы будем обозначать в дальнейшем символом 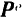
Выбор той или иной совокупности материальных точек (или тел) в качестве системы зависит от условий задачи. Следовательно, деление сил на внутренние и внешние также условно и зависит от того, что включено в состав рассматриваемой системы. Так, рассматривая движение поршня какого-либо, например автомобильного, двигателя и принимая поршень за отдельную систему, мы должны будем силы, действующие на него со стороны других звеньев механизма, считать внешними силами. Внутренними силами в этом случае будут лишь силы взаимодействия между частицами самого поршня. Принимая за систему весь кривошипно-шатунный механизм двигателя, мы должны уже отнести к внутренним силам и силы взаимодействия’ между отдельными его звеньями. Давление газов на поршень двигателя является по отношению к кривошипно-шатунному механизму внешней силой. Если же, рассматривая движение автомобиля в целом, принять за систему автомобиль вместе с двигателем, то для нее давление газов на поршень двигателя будет уже внутренней силой. Внешними силами такой системы будут: сила тяжести автомобиля, нормальная реакция дороги, сила трения между колесами автомобиля и дороги, сопротивление воздуха.
По закону равенства действия и противодействия, силы, с которыми действуют друг на друга две любые точки системы, равны по модулю и направлены по одной прямой в противоположные стороны. Геометрическая сумма этих сил, следовательно, равна нулю. Разбивая все внутренние силы системы попарно на равные по модулю и противоположные по направлению силы, мы приходим к следующим важным их свойствам.
- Главный вектор всех внутренних сил системы и алгебраические суммы их проекций на любые оси равны нулю:
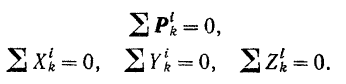
- Главный момент всех внутренних сил системы относительно любого центра и главный момент (алгебраическая сумма моментов) этих сил относительно любой оси равны нулю:
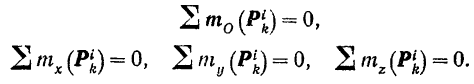
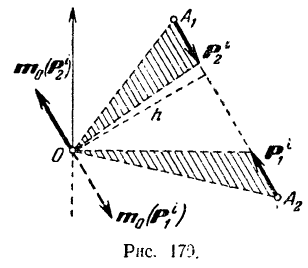
Действительно, построив (рис. 179) согласно известному правилу (§ 19) моменты сил взаимодействия 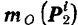 и
и 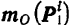 между двумя произвольными точками
между двумя произвольными точками 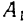 и
и 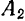 системы относительно любого центра
системы относительно любого центра 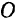 , найдем, что эти векторы равны по модулю (вследствие того, что силы
, найдем, что эти векторы равны по модулю (вследствие того, что силы 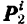 и
и 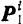 равны по модулю и имеют одинаковое плечо
равны по модулю и имеют одинаковое плечо 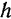 ) и противоположны по направлению. Складывая попарно моменты всех внутренних сил системы, мы приходим к равенству (136). Так как, по доказанному ранее (§ 32), проекция момента силы относительно точки на любую ось, проходящую через данную точку, равна моменту силы относительно этой оси, то из равенства (136) вытекают и равенства (137).
) и противоположны по направлению. Складывая попарно моменты всех внутренних сил системы, мы приходим к равенству (136). Так как, по доказанному ранее (§ 32), проекция момента силы относительно точки на любую ось, проходящую через данную точку, равна моменту силы относительно этой оси, то из равенства (136) вытекают и равенства (137).
Совокупность уравнений (134) и (136), так же как и уравнение (135) и (137), имеет вид уравнении равновесия произвольной пространственной системы сил. Однако отсюда не следует, что внутренние силы системы взаимно уравновешиваются. Они приложены к различным точкам (или телам) системы и могут вызывать их перемещения относительно друг друга. Уравновешиваются они только в случае, когда система представляет собой абсолютно твердое тело.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Затухающие колебания материальной точки с примером решения |
| Вынужденные колебания материальной точки с примером решения |
| Центр масс системы |
| Момент инерции тела относительно оси |

