Контрольная работа Д6.
Механическая система (рис. ДЗ, а) состоит из сплошного однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней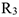 
и 
и 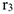радиусом инерции относительно оси вращения 
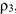, блока 4 и груза 5 (коэффициент трения груза о плоскость равен 
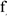). Тела системы соединены нитями, намотанными на шкив 3. К центру 
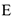блока 2 прикреплена пружина с коэффициентом жесткости 
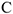; ее начальная деформация равна нулю.
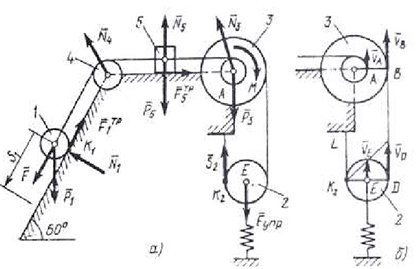
Система приходят в движение из состояния покоя под действием силы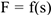 
, зависящей от перемещения 
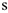точки ее приложения. На шкив 3 при движении действует постоянный момент 
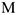сил сопротивления.
Дано:
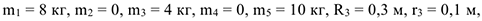
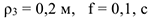
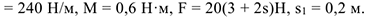
Определить: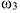 
в тот момент времени, когда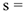 
.
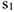Решение.
Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, соединенных нитями. Изобразим действующие не систему внешние силы: активные
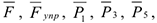
реакции
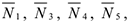
натяжение нити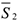 
, силы трения 
и момент .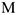
Для определения 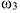воспользуемся теоремой об изменении кинетической энергии:
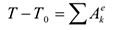
Определяем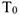 
и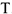 
. Так как в начальный момент система находилась в покос, то 
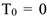. Величина 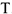равна сумме энергий всех тел системы:
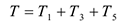
Учитывая, что тело 1 движется плоскопараллельно, тело 5 — поступательно, а тело 3 вращается вокруг неподвижной оси, получим
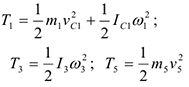
Все входящие сюда скорости надо выразить через искомую 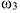. Для этого предварительно заметим, что
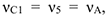
где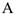 
— любая точка обода радиуса 
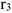шкива 3 и что точка 
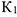— мгновенный центр скоростей катка 1, радиус которого обозначим 
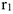. Тогда
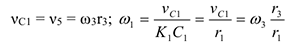
Кроме того, входящие в (3) моменты инерции имеют значения
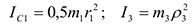
Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно
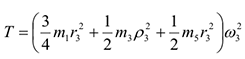
Теперь найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда центр катка 1 пройдет путь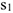 
. Введя обозначения: 
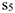— перемещение груза 
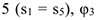— угол поворота шкива 
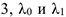— начальное и конечное удлинения пружины, получим
Работы остальных сил равны нулю, так как точк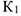и 
и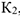
, где приложены силы 
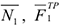и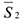 
— мгновенные центры скоростей; точки, где приложены силы 
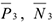и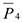 
— неподвижны; а реакция 
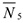перпендикулярна перемещению груза.
По условиям задачи,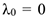 
. Тогда 
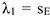, где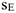 
— перемещение точки 
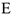(конца пружины). Величина 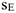и 
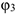надо выразить через заданное перемещение 
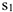; для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда так как 
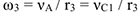(равенство 
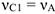уже отмечалось), то и 
.
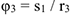Далее, из рис. Д3,б видно, что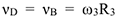 
, а так как точка 
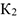является мгновенным центром скоростей для блока 2 (он как бы «катится» по участку 
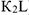), то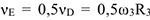 
; следовательно, и 
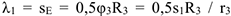. При найденных значениях 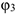и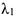 
для суммы вычисленных работ получим
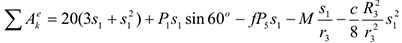
Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что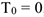 
, придем к равенству
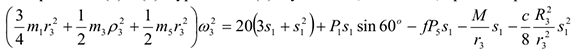
Из равенства (8), подставив в него числовые значения заданных величин, найдем искомую угловую скорость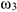 
.
Ответ: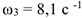 
.
