Оглавление:





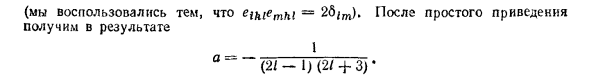

Матричные элементы векторов
- Матричные элементы векторов. Рассмотрим снова замкнутую систему частиц 1) и / Есть ли физический скаляр Значение. / Соответствует ли оператор этому количеству. Все скаляры инвариантны относительно поворота системы координат.
туземный Поэтому на скалярный оператор / это не влияет и меняется Есть операция вращения. Другими словами, обмен с оператором вращения. Однако оператор бесконечно малого вращения с точками равен С точностью до константы совпадает оператор мо Мужчины, так ^^ {/> L} = 0. (29,1)
Значение для переходов между состояниями Людмила Фирмаль
Оператор момента из коммутативного характера / / Mi с конкретными значениями L и M являются этими диагоналями Индекс. Кроме того, так как решено несколько задач M Направление системы только относительно координат Ось и скалярное значение от этого направления
Если это не зависит от этого, матричный элемент Вы (n! LM \ f \ nLM) не зависит от значения M (буква n условна В дополнение к L и M показаны все остальные наборы Число, определяющее состояние системы). официальный Доказательство этого утверждения можно получить с помощью: С учетом коммутативности операторов / и L +: fL + -L + f = 0. (29,2)
- Запишите матричные элементы этого уравнения для переходов n, L, M — y n ‘, L, M +1. Матрица L + n, L, M — y имеет только n, L, M + 1 элементов. (Ха, L, M + 1 | / | га, L, M + 1) (га, L, M + 1 | L + | ra, L, M) = = (M ‘, L, M + l | L + | ra’, L, M) (m ‘, L, M | / | m, L, M), Поскольку матричные элементы не зависят от индекса ха, тогда (Ха ‘, L, M + 1 | / | га, L, M + 1) = (ха’, L, M | / | га, L, M), (29,3) В общем, все (m /, L, M | / | m, L, M) c будут разными. ми М (и остальная часть того же индекса)
Самостоятельно Применяя этот результат к самому гамильтониану, Тогда мы получаем энергетическую независимость, которую мы уже знаем Устойчивое состояние М, т.е. (2L + 1) раз вырождается Энергетический уровень. Кроме того, пусть A будет векторной физической величиной на, особенность закрытой системы.
Компоненты вектора превращаются друг в друга Людмила Фирмаль
При включении системы Регулировки (особенно минимальное вращение, т.е. (под действием оператора момента). Так что в результате коммутации Оператор Ли с оператором Опять тот же компонент вектора Ai. Какой — может быть Однако в некоторых случаях А является Вам необходимо получить требуемый вектор частиц, уравнение (26.4).
так Поэтому правила переключения найдены. {Li, Ak} = ieikiAi. (29,4) Эти отношения могут дать много результатов Относительно матричной формы компонент вектора А (М. Борн, В. Гейзенберг, П. Иордания, 1926). Прежде всего, оказалось Вы можете найти правило выбора для определения Элементы матрицы движения могут быть ненулевыми.
нас Однако вместо цитирования соответствующего Хлопотный расчет позже выявил (§107) Эти правила на самом деле прямые Результаты общих конверсионных характеристик век Вы можете получить от них по существу Нет расчета. Вот правила Выход. Матричные элементы всех компонентов вектора Момент L Менее одного изменения. L ^ L, L ± 1 (29,5)
Кроме того, существуют дополнительные правила отбора для бана Общий переход между любыми двумя состояниями с L = 0. Это правило является очевидным результатом идеальной сферы Симметрия с нулевым моментом. Правило выбора для проекции момента М зависит от времени Векторный компонент.
То есть может быть ненулевым Матричные элементы для переходов со следующими изменениями ми значение М: M-y M 1 для Aj ^ -Ax — \ — bAy, M — >> M-1 для A_ = Az-gAy, (29,6) AZ MM. Кроме того, можно определить в общем виде Зависит от количества М матричных элементов в векторе. эти Вот некоторые важные и часто используемые формулы Потому что они реальны, без заключения
Более общие частные случаи (связанные с тензорами) Значение) отношений, приобретенных в § 107 Определены ненулевые матричные элементы Az Он делится по следующей формуле. (N’LM \ Az \ nLM) = VL {l + ^ L + 1) (n’L \\ A \\ nL), (N’LM \ A, \ n, L-l, M) = ^ ^ Ј ^ L-) {n’L \\ A \\ n, L-1), (29.7) (N ‘, L- \, M \ Aj \ nLM) = 1 | H || „L>. Вот символ (N’L ‘\\ A \\\ nL)
Показывает так называемые уменьшенные матричные элементы m s — это величина, которая не зависит от квантового числа M1). Они Связанные друг с другом отношениями (N ‘L’ \\ A \\ nL) = (nL \\ A \\ nfLf) *, (29,8) Сразу после Эрмита оператор Аз. Матрица, выраженная через те же элементы, что и данные Элементы величин A- и A +.
Ненулевая матрица Элементы А_ равны (N ‘, L, M-l \ A- \ nLM) = (N ‘, L, M-1 \ A- \ n, L-1, M) = (29-9) Матричный элемент A + не требует специального выражения. Из-за реальности Axe и Au (N L’M ‘\ A + \ nLM) = (nLM \ A- \ n L’M’) *. (29.10) Обратите внимание на выражение, которое представляет элемент матрицы ска Lar AV через редуцированный матричный элемент из двух векторов
Значения A и B. Расчет Оператор AB вида AB = \ (A + B- + A-B +) + AZBZ (29,11) Матрица величины AB (и скалярная) диагональна Л и М. Расчет с использованием (29,7) — (29,9) Результат: (N’LM \ AB \ nLM) = -V {riL \\ A \\ ri’L «) (n» L «\\ B \\ nL), 2L 1 ‘^ n «, L» (29,12) Где L выполняет значение L (L = b 1).
Написать матричные элементы для справки О векторе Л. Из сравнения уравнений (29.9) и (27.12) Мы идем (L \\ L \\ L) = y / L (L + l) (2L + l), (L-1 \\ L \\ L) = (L \\ L \\ L-1) = 0 (29,13) Что часто видно в приложениях Единичный вектор n в направлении вектора радиуса частицы. Найдите уменьшенный матричный элемент.
Для этого Например, рассчитать матричные элементы точно из nz = cos # Если момент проекции равен нулю: m = 0. 7G (/ -1, 0 | n ^ | / 0) = J @ i_10 cos 6 • @ u sin 6 d6 о Используйте функцию 0 / о (28.11). Интегральный расчет Результат 1) (/ -1, 0 | n J / 0) = il X’II / (2 / -1) (2 / + 1) Элемент матрицы перехода I —y I равен нулю ( Для полюсных векторов, связанных с отдельными Столица — см. Ниже (30,8).
По сравнению с (29,7) (L-l \\ n \\ l) = — (l \\ n \\ l-l) = iVi, (Z || n || Z) = 0. (29.14) Оспаривать Среднее тензорного PnPk- (1/3) 5ik (n Вектор радиуса частицы как заданное абсолютное значение) Вектор 1, но его направление (т. Е. Неопределенное lz).
Решения. Требуемое среднее значение — это оператор, который может: Представлено только оператором 1. ‘Tli’T ^ k Sik-CL _______2 Uh + hli- + 1) Это наиболее распространенный вид симметричного компонента 1 Тензор второго ранга с нулевым следом.
Определить постоянную Нет, но умножьте равенство, написанное слева, на U и г и к). Поскольку вектор n перпендикулярен вектору hi = [g], После этого u1% = 0.
Произведение hhlkh = (I2) 2 заменяется собственным значением. / 2 (/ + I) 2 и преобразовать произведение hlkhh, используя соотношение Переключите следующим образом (26.7): h lk h h = h h h h h-ieikihhh = (I2) 2 — e ik ih (k h-h k) = = (I2) 2 + K MelkmTtim = (T2) 2 -T2 = f (l + I) 2-1 (1 + 1) (Используется тот факт, что eiu ^ mki = 2 тусклый) — после простого броска В результате _________1 ~ (2 / -1) (2 / + 3) ‘
Смотрите также:
| Собственные значения момента | Четность состояния в физике |
| Собственные функции момента | Сложение моментов в квантовой механике |

