Оглавление:
Матричная запись системы линейных уравнений
Система 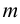 уравнений с
уравнений с 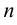 неизвестными
неизвестными 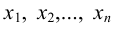 называется линейной, если она имеет вид
называется линейной, если она имеет вид
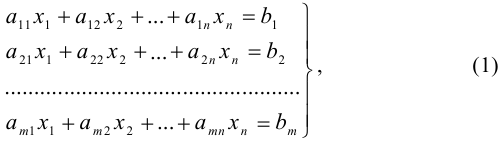
где 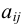 ,
, 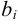 (
(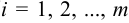 ;
; 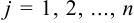 ) — числа, причем для каждого
) — числа, причем для каждого 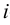 имеется хотя бы одно
имеется хотя бы одно 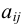 , отличное от нуля.
, отличное от нуля.
Матрица
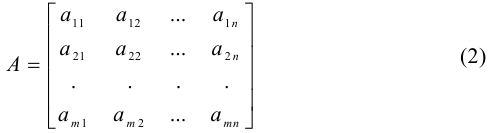
называется матрицей системы, а матрица
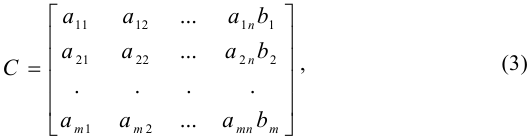
которая получается из матрицы  приписыванием столбца из свободных членов — расширенной матрицей системы.
приписыванием столбца из свободных членов — расширенной матрицей системы.
Систему (1) можно записать в матричном виде  , где
, где  имеет вид (2);
имеет вид (2);
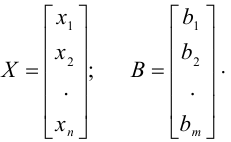
Систему (1) можно записать также в виде
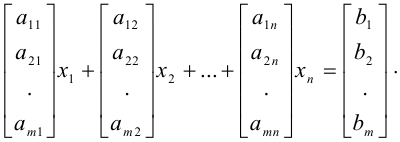
Теорема Кронекера-Капелли
Система называется совместной, если существует хотя бы одно решение этой системы. В противном случае система называется несовместной.
Совместная система называется определенной, если она имеет единственное решение. Система, имеющая более одного решения, называется неопределенной.
Теорема. Система из  уравнений с
уравнений с  неизвестными совместна тогда и только тогда, когда ранг матрицы
неизвестными совместна тогда и только тогда, когда ранг матрицы  равен рангу расширенной матрицы
равен рангу расширенной матрицы 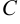 . При этом, если ранг
. При этом, если ранг 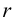 обеих матриц равен числу неизвестных, т. е.
обеих матриц равен числу неизвестных, т. е. 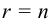 , то система имеет единственное решение. Если же
, то система имеет единственное решение. Если же 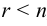 , то система имеет бесконечное множество решений.
, то система имеет бесконечное множество решений.
Правило Крамера
Рассмотрим систему 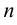 линейных уравнений с
линейных уравнений с 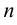 неизвестными
неизвестными
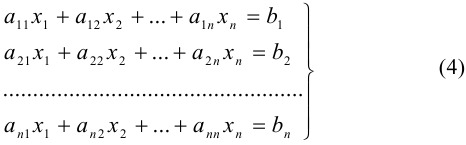
Матрица  такой системы является квадратной матрицей порядка
такой системы является квадратной матрицей порядка 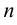 . Определитель этой матрицы
. Определитель этой матрицы
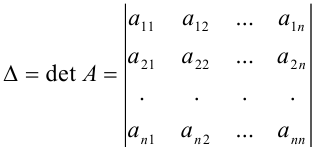
называется определителем системы (4).
Невырожденная система 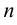 линейных уравнений с
линейных уравнений с 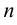 неизвестными имеет единственное решение, которое может быть найдено по формулам Крамера:
неизвестными имеет единственное решение, которое может быть найдено по формулам Крамера:
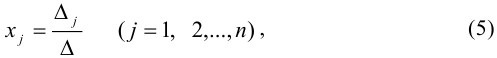
где 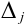 — определитель, полученный из определителя
— определитель, полученный из определителя  заменой
заменой 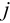 -го столбца столбцом из свободных членов системы.
-го столбца столбцом из свободных членов системы.
Матричное решение системы линейных уравнений
Запишем систему линейных уравнений (4) в матричном виде  . Предположим, что
. Предположим, что 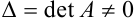 . В этом случае матрица
. В этом случае матрица  имеет обратную матрицу
имеет обратную матрицу 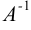 такую, что
такую, что 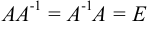 . Умножим обе части уравнения
. Умножим обе части уравнения  слева на
слева на 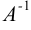 . Получим
. Получим
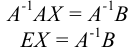
Решение системы линейных уравнений имеет вид:

где  и
и 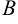 — матрицы-столбцы;
— матрицы-столбцы; 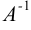 — матрица, обратная матрице системы.
— матрица, обратная матрице системы.
Метод нахождения решения системы с использованием формулы (6) назовем матричным.
Задача №8.
Выяснить, является ли система
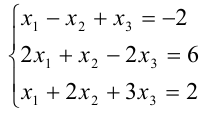
невырожденной, и если является, то решить ее по формулам Крамера (5).
Решение:
Так как определитель данной системы
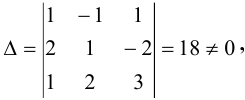
то система является невырожденной.
Для того чтобы воспользоваться формулами Крамера (5), находим:
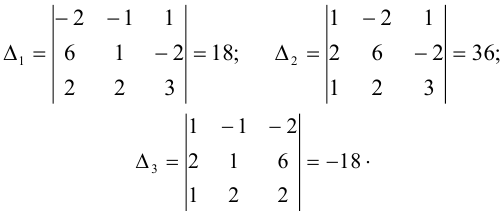
Подставляя в (5) значения 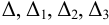 , имеем:
, имеем: 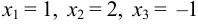 .
.
Задача №9.
Решить матричным методом систему
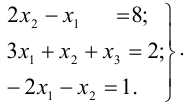
Решение:
Для данной системы основная матрица
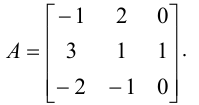
Обратная матрица
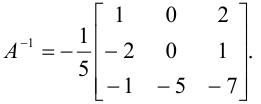
По формуле (6)
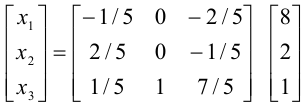
или
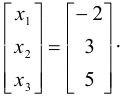
Отсюда 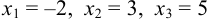 .
.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Обратная матрица с решением задачи |
| Ранг матрицы задачи с решением |
| Решение произвольных систем матриц задача с решением |
| Метод последовательного исключения неизвестных (метод Гаусса) задачи с решением |

