Система уравнений по методу непосредственного применения законов Кирхгофа может быть записана в матричной форме. Для чего перепишем уравнения (3.25), (3.27) упорядоченно по номерам токов, а если данного номера тока нет, запишем данный ток умноженным на нуль:
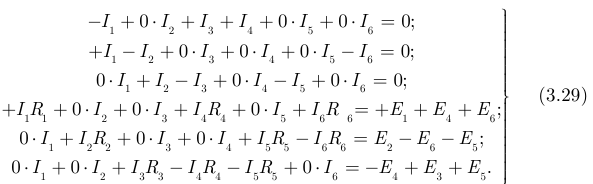
Последняя система (3.29) в матричной форме:
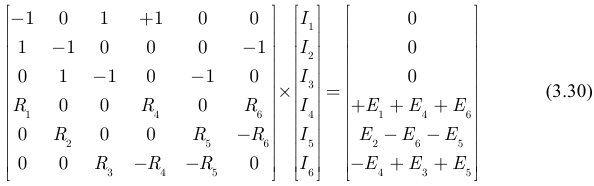
Краткая система записи последнего выражения имеет вид:

где 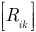 — квадратная матрица обобщенных сопротивлений по методу законов Кирхгофа;
— квадратная матрица обобщенных сопротивлений по методу законов Кирхгофа; 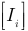 — матрица-столбец неизвестных токов;
— матрица-столбец неизвестных токов; 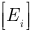 — матрица-столбец обобщенных ЭДС метода непосредственного применения законов Кирхгофа;
— матрица-столбец обобщенных ЭДС метода непосредственного применения законов Кирхгофа; 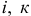 — соответственно номера рядов и столбцов элементов матриц.
— соответственно номера рядов и столбцов элементов матриц.
Матрицу токов в системе (3.31) можно найти с помощью обратной матрицы обобщенных сопротивлений:

Применение матриц позволяет кратко записать уравнения, но общий объем вычислений не уменьшается.
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:
| Эквивалентные преобразования участков цепи с источниками энергии |
| Метод непосредственного применения законов Кирхгофа |
| Метод контурных токов (MKT) |
| Метод узловых потенциалов (МУП) |
