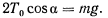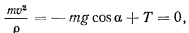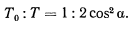Задача №55.
Материальная точка весом  подвешена при помощи двух одинаковых нитей к двум опорам, находящимся на одном и том же горизонтальном уровне, причем угол наклона каждой нити к вертикали равен
подвешена при помощи двух одинаковых нитей к двум опорам, находящимся на одном и том же горизонтальном уровне, причем угол наклона каждой нити к вертикали равен 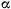 . Внезапно одну из нитей перерезают. Доказать, что натяжение другой нити мгновенно изменится в отношении
. Внезапно одну из нитей перерезают. Доказать, что натяжение другой нити мгновенно изменится в отношении 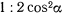 .
.
Решение:
В положении равновесия имеет место условие
После обрыва нити уравнение движения точки в проекции на нормаль получит вид
откуда будем иметь
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
| Задача №53. Тяжелая материальная точка движется по внутренней поверхности прямого кругового конуса, вершина которого обращена вниз, а ось симметрии вертикальна. Угол при вершине равен . В начальный момент расстояние точки от вершины конуса равно , начальная скорость равна и направлена перпендикулярно к образующей конуса. Определить траекторию точки и давление, которое она оказывает на поверхность конуса. |
| Задача №54. Тяжелая материальная точка вынуждена оставаться на совершенно гладкой плоскости, которая равномерно вращается вокруг горизонтальной оси, расположенной в самой плоскости. В начальный момент точка находится на оси вращения, а ее скорость направлена вдоль оси вращения и равна . Определить закон движения точки. |
| Задача №56. Материальная точка совершает колебания на гладкой параболе с вертикальной осью, изменяя направление своего движения на концах хорды, проходящей через фокус параболы перпендикулярно к оси параболы. Найти давление точки на параболу в самой нижней точке. |
| Задача №57. По лемнискате, уравнение которой , скользит вниз от вершины весомая материальная точка , начиная движение без начальной скорости. Определить время движения до точки в зависимости от угла при отсутствии трения. |

 подвешена при помощи двух одинаковых нитей к двум опорам, находящимся на одном и том же горизонтальном уровне, причем угол наклона каждой нити к вертикали равен
подвешена при помощи двух одинаковых нитей к двум опорам, находящимся на одном и том же горизонтальном уровне, причем угол наклона каждой нити к вертикали равен 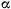 . Внезапно одну из нитей перерезают. Доказать, что натяжение другой нити мгновенно изменится в отношении
. Внезапно одну из нитей перерезают. Доказать, что натяжение другой нити мгновенно изменится в отношении 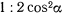 .
.