Материальная точка массы притягивается неподвижным центром с силой

Задача №45.

Материальная точка 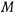массы 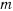притягивается неподвижным центром 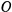с силой 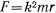, где 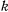— постоянный коэффициент пропорциональности, 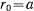— расстояние точки 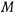от 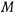. В начальный момент расстояние 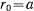, а скорость образует с направлением 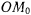угол 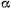. Найти уравнения движения точки и ее траекторию, принимая прямую 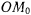за ось .

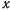Решение:

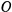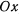Выберем систему неподвижных осей с началом в центре притяжения . Ось направим так, чтобы она проходила через начальное положение точки. Сила 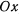, действующая на точку, будет направлена по оси 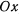, и если бы начальная скорость точки была направлена вдоль оси 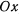, точка совершала бы прямолинейное движение. Но направление начальной скорости не совпадает с направлением оси 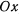, а потому точка покидает ось 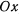и будет совершать некоторое плоское движение. Сила в каждый момент времени будет направлена к притягивающему центру и проекции этой силы на оси координат будут иметь вид

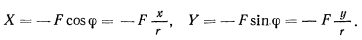
Подставляя сюда значение силы , получим

после чего уравнения движения запишутся в виде

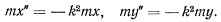
Уравнения эти могут быть проинтегрированы независимо одно от другого. В результате получаем общее решение системы

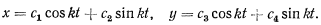
Из начальных условий имеем

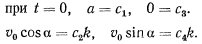
Так что движение будет происходить по закону

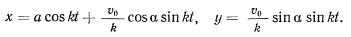
Исключая из этих уравнений время, получим уравнение траектории

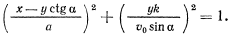
Задача взята со страницы подробного решения задач по всем темам теоретической механики:

Решение задач по теоретической механике

Возможно эти дополнительные задачи вам будут полезны:

Задача №43. На негладкой горизонтальной плоскости лежит полушар весом и с радиусом . В точке на него действует горизонтальная сила . Зная значение коэффициента трения между полушаром и опорной плоскостью, определить условия равновесия полушара, если расстояние (рис. 47).

Задача №44. Пусть ось направлена вертикально вверх. Будем предполагать, что на материальную точку действует только сила тяжести. Проекция силы тяжести на ось будет постоянна по величине и имеет отрицательное значение —. Поэтому движение материальной точки вдоль оси будет определяться дифференциальным уравнением.

Задача №46. Материальная точка совершает плоское движение под действием некоторой силы , причем траектория точки оказывается эллипсом а ее ускорение все время остается параллельным оси . В начальный момент точка находится на оси , а ее скорость равна . Определить силу» действующую на точку, в функции координат точки.

Задача №47. С крепостной башни производят два выстрела, причем начальные скорости снарядов оказываются равными по величине и лежат в одной и той же вертикальной плоскости. Эти начальные скорости направлены под углами и к горизонту. Оба снаряда попадают в одну и ту же точку на поверхности Земли. Найти высоту башни, предполагая, что поверхность Земли вокруг башни горизонтальна и что сопротивление воздуха отсутствует.