Задача №59.
Математический маятник подвешен внутри вагона, движущегося по прямолинейным рельсам с постоянным ускорением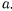 
. Определить период колебаний маятника, предполагая, что нить, на которой подвешен маятник, нерастяжима и имеет длину 
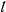(рис. 62).
Решение:
Маятник совершает колебания относительно системы отсчета, связанной с движущимся вагоном. При изучении движения относительно такой системы к действующим силам необходимо добавить силы инерции Кориолиса. Подвижная система, связанная с вагоном, движется поступательно, а потому сила Кориолиса от добавочного ускорения будет равна нулю. Сила Кориолиса от переносного ускорения будет равна 
, так как система движется с ускорением. Добавляя силу Кориолиса к силе тяжести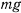 
, получим результирующую силу 
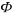, действующую на точку в подвижной системе отсчета, величина которой определяется равенством
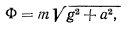
а направление ее составляет угол 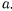с вертикалью. Величина угла определяется равенством
Нетрудно видеть, что в рассматриваемой системе координат на точку действует постоянная по величине и по направлению сила 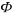. Ранее мы видели, что под действием такой силы маятник совершает колебательное движение около положения равновесия, в котором направление нити совпадает с направлением силы, а период колебаний определяется формулой
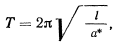
где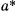 
— ускорение, сообщаемое силой свободной материальной точке. В нашем случае это ускорение 
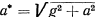, поэтому искомый период
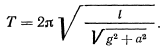
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
