Масса плоской пластинки

Масса плоской пластинки

Требуется найти массу 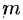плоской пластинки , зная, что ее поверхностная плотность 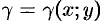есть непрерывная функция координат точки 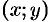. Разобьем пластинку на элементарных частей 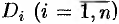, площади которых обозначим через 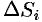. В каждой области 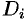возьмем произвольную точку 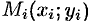и вычислим плотность в ней: .

Если области 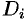достаточно малы, то плотность в каждой точке мало отличается от значения . Считая приближенно плотность в каждой точке области 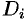постоянной, равной , можно найти ее массу . Так как масса 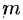всей пластинки равна , то для ее вычисления имеем приближенное равенство

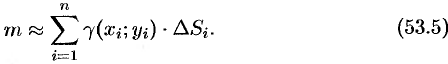
Точное значение массы получим как предел суммы (53.5) при услови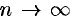и и :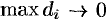

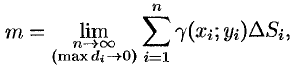
или, согласно равенству (53.2),

Итак, двойной интеграл от функции численно равен массе пластинки, если подынтегральную функцию считать плотностью этой пластинки в точке 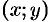. В этом состоит физический смысл двойного интеграла.

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Системы линейных ДУ с постоянными коэффициентами

Объем цилиндрического тела

Вычисление двойного интеграла в декартовых координатах

Вычисление двойного интеграла в полярных координатах