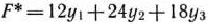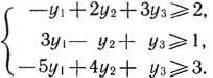Задача 1.77.
Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции
при условиях
Решение:
Для данной задачи
Число переменных в двойственной задаче равно числу уравнений в системе (59), т. е. равно трем. Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений (59), т.е. числа 12, 24, ]8,
Целевая функция исходной задачи (58)—(60) исследуется на максимум, а система условий (59) содержит только уравнения. Поэтому в двойственной задаче целевая функция исследуется на минимум, а ее переменные могут принимать любые значения (в том числе и отрицательные). Так как все три переменные исходной задачи (58)—(60) принимают только лишь неотрицательные значения, то в системе условий двойственной задачи должны быть три неравенства вида 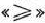 . Следовательно, для задачи (58)—(60) двойственная задача такова: найти минимум функции
. Следовательно, для задачи (58)—(60) двойственная задача такова: найти минимум функции
при условиях
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
| Задача 1.66. На ткацкой фабрике для изготовления трех артикулов ткани используются ткацкие станки двух типов, пряжа и красители. В табл. 1.36 указаны производительность станков каждого типа, нормы расхода пряжи и красителей, цена 1 м ткани данного артикула, а также общий фонд рабочего времени станков каждого типа, имеющиеся в распоряжении фабрики фонды пряжи и красителей и ограничения на возможный выпуск тканей данного артикула. |
| Задача 1.67. Машиностроительное предприятие для изготовления четырех видов продукции использует токарное, фрезерное, сверлильное, расточное и шлифовальное оборудование, а также комплектующие изделия. Кроме того, сборка изделий требует выполнения определенных сборочно-наладочных работ. Нормы затрат всех видов ресурсов на изготовление каждого из изделий приведены в табл. 1.39. В этой же таблице указаны наличный фонд каждого из ресурсов, прибыль от реализации единицы продукции данного вида, а также ограничения на возможный выпуск продукции 2-го и 3-вида. |
| Задача 1.78. Для задачи, состоящей в максимизации функции |
| Задача 1.87. Для задачи, состоящей в определении максимального значения функции |

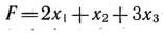
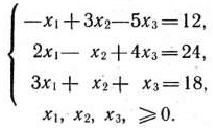
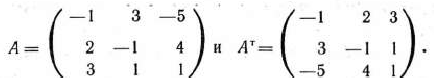
 . Следовательно, для задачи (58)—(60) двойственная задача такова: найти минимум функции
. Следовательно, для задачи (58)—(60) двойственная задача такова: найти минимум функции