Оглавление:
Малые свободные колебания системы
Свободными колебаниями называется колебательное движение системы, выведенной из положения равновесия и предоставленной самой себе. Составим уравнение Лагранжа для консервативной системы
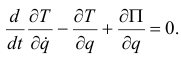
Используя (20.4) и (20.5), получим дифференциальное уравнение свободных колебаний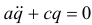 
или, обозначив 
,
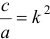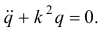
Решение этого однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами известно
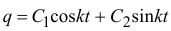
или, использовав другие постоянные
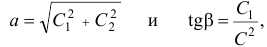
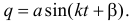
Следовательно, малые свободные колебания — гармонические колебания, причем амплитуда колебаний и начальная фаза определяются начальными условиями (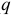
и 
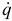при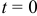 
), а частота колебаний 
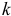и период 
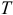не зависят от начальных условий, определяются только конструкцией системы. Обычно частоту колебаний находят сравнением полученного дифференциального уравнения с уравнением (20.6).
Пример:
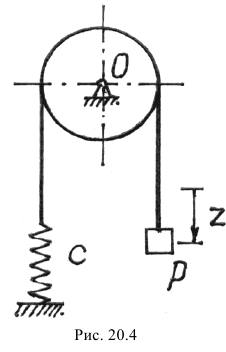
Тело весом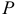 
подвешено на нити, перекинутой через блок и прикрепленной к пружине (рис. 20.4). Вес блока 
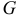, радиус — 
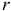; жесткость пружины 
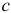. Определим период свободных колебаний системы.
Назначим обобщенной координатой смещение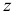 
груза по вертикали от положения равновесия, при котором пружина была растянута на величину 
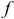. Тогда потенциальная энергия относительно положения равновесия
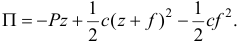
Где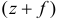 
— полная деформация пружины, а 
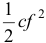— потенциальная энергия пружины в положении равновесия, которую вычитаем из потенциальной энергии полностью деформированной пружины. Раскрыв скобки, получим:
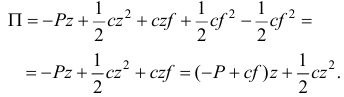
В положении равновесия должно выполняться условие
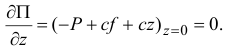
Отсюда
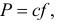
значит,
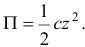
Кинетическая энергия системы
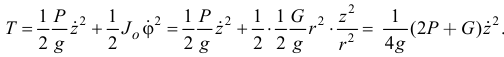
Сравнивая с формулой Лагранжа, получим:
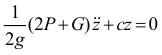
или
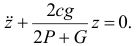
Сравнивая с формулой (20.6), находим частоту колебаний
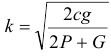
и затем период
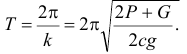
Пример:
Определим период малых колебаний балочки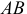 
на цилиндрической поверхности (см. пример 18.4).
Потенциальная и кинетическая энергии определены. Разложим их в ряд с точностью до малых величин второго порядка. Для этого достаточно положить
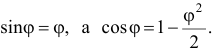
Получим
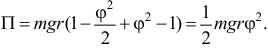
Кинетическая энергия получится такой, если отбросить член четвертого порядка, содержащий произведение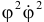 
:
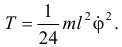
Составляем уравнение Лагранжа. Определив производные
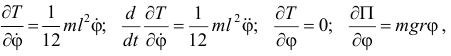
получим уравнение
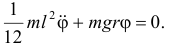
Приводим к его к форме (20.6):
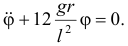
Поэтому частота малых колебаний
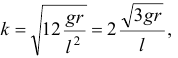
а период
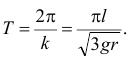
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Дифференциальные уравнения плоскопараллельного движения тела |
| Основные определения колебательного движения |
| Свободные колебания системы с учетом сил сопротивления движению |
| Вынужденные колебания системы |
