Оглавление:













Малые колебания
- Рассмотрим систему с независимыми от времени соединениями, как описано выше. Его положение зависит от геометрических параметров k или qv q2…. Все силы зависят от всех переменных Q силовых функций U q2, q2,…функция равна нулю, а все переменные q y = 1, 2… …. А исчезнет. Соответствующее положение равновесия является стабильным. Была поставлена задача изучить малое движение системы вокруг этого position. Эти небольшие ходы, количество qt, q2……. дь, и Скорость остается очень высокой low. В результате дифференциал q , q 2…….
Кинетическая энергия gia является существенно положительной однородной функцией 2 го порядка относительно производной q В этом случае, если есть полное подключение к системе. 1.Полностью подключенная система. Расположение системы в рассматриваемом случае зависит от 1 параметра Q. Это, по предположению, будет равно нулю в положении равновесия. Число а равно 1.Кинетическая энергия T является 2 й однородной функцией переменной Q и имеет следующий вид: Т 7i1 = о + г га +.
По теореме Гюйгенса массы можно подобрать так, чтобы периоды колебаний вокруг обеих осей были одинаковы, и этот общий период будет периодом колебаний математического маятника, длина которого равна расстоянию между ребрами ножей. Людмила Фирмаль
Здесь предполагается, что функция f q расширяется в ряду Маклорина. Предположим, что первый член разложения 0 не равен нулю. Для очень малого q кинетическая энергия T, которая практически положительна, имеет знак пункта 1 0, поэтому этот пункт 1 0 обязательно будет положительным. Множество f 0 = a Писать о 8 + л T содержит фактор qg и поэтому очень мал по сравнению с первым членом. Теперь рассмотрим функцию силы U.
Предположение, что это функция q, которая обращается в нуль и имеет максимальное значение. Русский перевод этой статьи будет впервые опубликован во 2 м издании общего номера Гостехиздат. Примечание, транс Наиболее распространенные случаи рассмотрены в книге: Четаев Н. Г. устойчивость движения, Гостехиздат, 1946. Примечание, транс если q = 0.So, если поместить U = F q и F q в ряд Маклорена, то P 0 и F 0 будут равны нулю, а F 0, в общем случае, будут отрицательными. F Q = , предполагая a 0 Вот сумма последующих терминов Маклорина decomposition. As в результате Ut содержит коэффициент 7, и поэтому очень мал по сравнению с термином aq2.
Чтобы узнать малую вибрацию, игнорируйте количество T1 и V Т = АД у = aq2. Тогда уравнения движения Лагранжа Л йй йй dt Поскольку он равен нулю, он выглядит так: р р р р, 7 = r2q, я Вот, поставьте = r2.Интегрирование этого уравнения г = kcos р 4 П Кир указывает начальное положение, то есть величину 0 0, и 2 произвольные константы, определяемые начальной скоростью q0.Период колебаний системы равен. Константа r, имеющая конкретное физическое значение, очевидно, не зависит от выбора параметра Q. Если начальные значения равны q и q. если t = 0, то это a и b2. м = с, Потому что РТ + грех РТ.
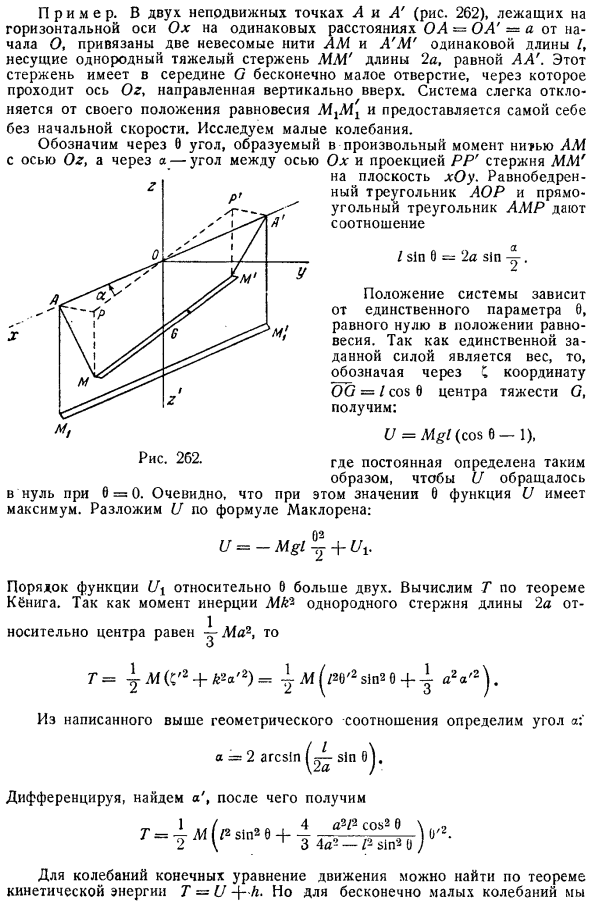
В других случаях начальными значениями q и q являются a2 и b2.Затем, для того же движения м = если в J2, потому что РТ + РТ грех. Наконец, в 3 м случае, если начальные значения q и q равны b, то соответствующее выражение q Вы будете 7 = я + 2 потому что РТ + Дж Грех РТ Это будет предыдущая сумма 2.Эта характеристика, являющаяся результатом линейности уравнений движения, называется суперпозицией малых колебаний. Образцы. 2 неподвижные точки A и A рис.262 на горизонтальной оси Ox равноудаленные O A = OA = начиная от a и от O той же длины Z 2 невзвешенные нити AM и a M крепятся и стержень мм длины 2a равен равномерному тяжелому AA.
В этом стержне, в середине G, имеется микроотверстие, через которое ось Og проходит вертикально вверх. Система немного отклоняется от положения равновесия MtMt и остается неповрежденной без начальной скорости. Исследуйте небольшие колебания. Угол, образуемый в любой момент поток АМ 0.Это угол между проекцией PP стержня LMG на плоскости Ox и xOy. Равнобедренные AOR и AMR прямоугольного треугольника дают соотношение 0 = от 0 до нуля. Очевидно, самый большой. разверните U в Phi Положение системы зависит от одного параметра O, который равен нулю в положении равновесия.
Поскольку заданная сила является только весом, координаты обозначаются буквой С, а координаты центра тяжести О. У = Мгал потому 6 1 Константа определяется так, что U обращается к 0, а функция U имеет Маклорин. У = Уй МГЛ +. Порядок пользовательского интерфейса для функции 9 больше 2.Теорема Кенига вычисляет т.
Момент инерции к центру однородного стержня длины 2a равен Ma2 Р = г л С + Gv 2 = 1 Л п29 2 sin2 9 + г Из приведенных выше геометрических соотношений определим угол a: a = 2 arcsin sin 9y Когда вы различаете, найдено и затем а2р потому что о В случае конечных колебаний уравнение движения можно найти в теореме о кинетической энергии T = 1 f L. Но в случае бесконечно малых колебаний Установите коэффициент в Формуле Ch 2, полученной для T, приравнивая значение при 8 = 0, приблизительно Т = Затем уравнения движения, основанные на уравнении Лагранжа Период малых колебаний Заметим, что если форма имеет равна q 2 F Q выше, я предположил, что F 0 не равно нулю.
Если это условие не выполняется, его можно реализовать путем преобразования variable. In факт, малый q Ф Щ = 9 г. Куда 0 не равно нулю. Давайте сделаем замену. Где S новая переменная. У нас есть Р = 2 Н ф г = коэффициенты s 2 больше не применяются Кроме того, если коэффициент qri в Формуле, полученной для T, не исчезает при q = 0, то U Начинается экспансия в разделе 2 квартале на официальном Маклорена.
Однако если максимальное значение U q равно q = 0, то все производные от U в некоторой нечетной степени выше первой производной, а первая ненулевая производная Четна и отрицательна. Например, в простейшем случае, это может произойти в следующих случаях У м ах + УБ Где Uj содержит фактор q , а коэффициент a положителен. Тогда, если мы приведем T к виду aq 2 и проигнорируем член Uy, мы получим уравнение. 2 р р = р р. В этом случае возникают особые ситуации, которые не зависят от выбора переменных. Период малых колебаний вблизи положения равновесия изменяется с течением времени. amplitude. In фактически, мы предоставляем систему, помещая ее в положение, соответствующее qe.
Сама, без начальной скорости. Если мы интегрируем уравнение 2 = Здесь мы определяем t в функции q с эллиптичностью. значения q q и 4 Период изменения и квартал между П. Период колебаний равен Где q = sq помещается. Следовательно, этот период обратно пропорционален q0 и бесконечно велик, если q0 стремится к нулю. 2. Система с 2 степенями свободы. Представьте себе систему с независимой от времени связью.
Его положение определяется двумя параметрами: qx и q2.У нас есть T = Aq 2 J 2Bq q J Cq Где A, B, C функции q и q2. Параметр предполагает, что дискриминант AC B2 выбран таким образом, что он не исчезает с qt = q2 = 0.In в свою очередь, коэффициенты ряда Маклорина A, B. разверните C и укажите a, b. Если значение этих коэффициентов равно gi = g2 = 0, то получим: Т = р р 2И 2dgjg 4 + а Где 7 Количество 3 го порядка для g, q2, q R q и исчезает с qt = q2 = 0.So, если q и q2 очень малы, то T имеет знак 3 членов, обращенных к T. независимо от d и d are, потому что T положительно по своей природе в 0, 0. В2 ас 0. Теперь рассмотрим силовую функцию U qv q2.
Если gi = g2 = 0, то эта функция гасится и имеет максимальное значение. Поэтому, если мы расширим его в серию Маклорина, мы сможем увидеть: У = д 4 2 й, д. 4 Д 4 с,,, Где Ut q и количество 3 го порядка около q2. что касается полностью малых значений qt и q2, U должен быть отрицательным 0, 7, 0. 0. Игнорируйте функции T и Ul, чтобы получить небольшие колебания вблизи положения равновесия. Т = = agj2 4 2ftgjg 4 СД 1 У = ад2 4 tyqrfi 4 7 д. 3 4 Затем оба уравнения Лагранжа преобразуются в линейное уравнение с постоянными коэффициентами М + bq2 = AQT по 4 Кварты, 1 b4i + cq 2 = Qqi + vhY J Чтобы интегрировать эти уравнения 9и = k1Cos РТ + Р. К2 = XJ в кос РТ 4 П.
- Где kj, Xj, r, p константы. Подставляя эти значения в уравнение 3 и уменьшая их с помощью cos rt p и XDag ч ХС М П = 0, х, м —р 4 Х2 Н Р =0. 5. Отсюда, за исключением Xt, мы получаем квадратное уравнение. ар н — 7 м р = 0, 6 Левая сторона равенства 6 положительна, если r2 равен 0 и 4 oo, и отрицательна, если r2 равен и, поэтому r2 имеет 2 действительных и положительных значения. Поскольку решение в 4 не изменяется при изменении знаков r и p, r всегда можно считать positive. So, для r и rg мы можем взять 6 положительных корней Формулы 2. если заменить r на 1 из этих маршрутов в уравнениях 5, то они сводятся к 1 уравнению, например первому.
Затем, когда R r1: установлен, он выглядит так: Где p любая константа. Таким образом, получается решение я = Л Я Г, потому что Риз + Пи ЧР = л я —или Ф Т 4 Р1. 2 й маршрут gj дает аналогичное решение в других константах pg и pg и, наконец, получает общий Интеграл уравнений движения. 41 = 1 1 В2, потому что Р + ро б ПГ бк2 Р соз Р2 4 П2. Один Р = Р1 АР С ув Привет + Л 2 со + л. с. Он содержит 4 произвольные константы px, pj, pt и pr. Они определяются, когда известны начальные значения параметров QT и q2 и их производные q X и q2. Таким образом, можно видеть, что движение вблизи положения равновесия является результирующим движением периодических 2 колебаний. 2р 2 й Каждый равен и.
Один из цилиндров полый, а другой заполнен свинцом, так что центр тяжести расположен ближе к одному ножу, чем к другому. Людмила Фирмаль
Если эти периоды взаимно уравновешены, то движения носят периодический характер. В противном случае система не будет проходить через одну и ту же позицию 2 раза. Мы уже видели подобные примеры в пункте 272. Величины rt и r2, имеющие определенное физическое значение, очевидно, не зависят от выбора параметров QT и q2.Они являются инвариантами задачи. Особый случай.
Когда мы доказали, что в уравнении 6 есть 2 положительных корня относительно gy, мы предположили, что подстановка и в левую часть уравнения даст it. At минимум 1 раз это отрицательное значение. Если это не так Н = 4 1 Где k2 положительная постоянная. Уравнение 6 имеет вид r2 L2 2 = 0. И у него будет 2 равных корня. Тем не менее, общий интеграл не включает t вне синуса и cosine.
Дело в том, что при рассматриваемых условиях уравнение движения 3 принимает вид: + G91 относительные + Б 4 А2 2 = 0 Б БПФ + fe29i 4 с Н2 2 р Р = 0 поскольку d2 ac положителен, эти уравнения выглядят следующим образом: 4 = 0. 7 + la9r = о С этого момента общие интегралы 9и = HC0S ж + Пи 92 = P2c 8 а + Р2. В настоящее время есть только 1 период в качели. Другой способ. Если вы используете свойства квадратичной формы, эти результаты могут быть получены другим способом. 2.
Рассмотрим 2 й формат Ы =клок+ 2b4lq2 + СЧ, у= + 2р Я 72 + с При этом уравнение движения можно записать в виде: dU dS dU dt lql = dqC dt dq2 = dq2 Давайте сделаем линейную подстановку 4 1 2 2 = 4 Где Si и s2 новые параметры, а KT, hl, k2 константы. Вы можете определить коэффициент замещения, чтобы суммировать обе формы квадратов одновременно. если вы рассматриваете рассматривать2 как декартову координату, это то же самое, что взять прямую линию в качестве оси. Это сопряжено с парой S = 0 линии в то же время. У=О.
Кинетическая энергия изменяется на T = s + s2, и уравнение движения принимает вид: При интеграции вы увидите следующее: Си = Пт, потому что РЖ + Р1, СС = Р2 соз Р Джей + Р2. можно отметить, что получено билокадебраическое уравнение r , а дискриминант в виде U r2S равен нулю. Переменные St и s2 называются основными переменными. Приложение. Рассмотрим однородный i стержень AB 2A фиксируется с помощью подвесного Рис. 263.Система движется по вертикали xOy plane. It необходимо найти микровибрацию вблизи вертикали, которая является положением равновесия. Положение системы зависит от 2 углов 0, вертикальный Вол образуется направлением hi и стержнем.
Эти параметры действительно исчезают в состоянии равновесия. Есть функция питания У = Мг С Где 6 абсцисса центроида G. согласно предыдущей теории, константа C должна быть упорядочена так, чтобы она исчезла в положении равновесия. Координаты центроида 5 = З cos0 значение COS р, ч = я 0 4 грех грех, если. Функции У = мг я потому что в 1 й 2 C0S П 1. Теперь рассчитаем кинетическую энергию t. кинетическая энергия массы M сосредоточена в центре тяжести O М 6 2 + г г = 1 m число+ а 2 + 2aH не потому что 0 р 1.
Зная выражение момента инерции относительно центра однородного стержня, можно получить кинетическую энергию вращательного движения В переменных Sj и s2 чаще встречаются имена lava или стандартные координаты. Примечание, Пер Значение вокруг центроида является значением я АФА З 2.Поэтому полная кинетическая энергия r B 2 + A a3T 2 + 2a 9 е, потому что в Чтобы найти микровибрации, достаточно получить только 2 й порядок U и T. Год+ = T = z = 6 2 + vzT 2 + 2019. И уравнение Лагранжа 28 + Альф = gl9, АФИ + ал9 = гей. Чтобы интегрировать эти уравнения 0 = кДж соз г + р, м= .2 со г 4 П. Константа и X2, условие r3 k1 + ar2X3 = o, r2X1 + in Итак, для r2 вы получаете уравнение 0.
Уравнение 2 го порядка этого r3 имеет 12 действительных положительных корней, каждый из которых соответствует определенной системе решений. Добавьте эти решения, чтобы получить общие интегралы 6 = АРФП, потому что Р, Ф + П1 + l2p2 потому что Р, Ф + Пэ ты можешь это сделать. потому что г + П1 + г Irj в COS Г2 + ПГ В том числе 4 Например, если вы хотите получить значение 2+ 1 3 2 3 из него образуется цикл обоих колебаний, из которого составляются и берутся непосредственно малые движения. Обратите внимание, что предыдущая теория предполагала, что ac 6 не равен нулю. Если этот дискриминант равен нулю, то параметры следует выбирать по разному.
Это означает, что новое приближенное выражение для энергии T имеет дискриминант, который не равен нулю. Например, если вы перемещаетесь по плоскости и берете точку с устойчивым положением равновесия в начале координат, координаты изгиба будут равны T Дженни. Дискриминант, в котором r3 исчезает в положении равновесия. Когда вы получаете декартовы координаты, вы получаете новую формулу Этот дискриминант не равен нулю. Мы также предположили, что разложение силовой функции U начинается с членов 2 го порядка для q и q2.Разложение функции U начинается с члена четного порядка так как U O является наибольшим, но, например, 4 го и т.
В этом случае исследование малых колебаний усложняется, так как игнорируя член Ut, полученное уравнение перестает быть линейным. Общее движение перестает быть результатом 2 х особых колебаний, каждое из которых имеет определенный промежуток времени. 3.Общий случай. Рассмотрим систему, которая подвергается независимой от времени связи и находится под действием силы с функцией силы U. предположим, что существует устойчивое положение равновесия системы, в котором функция U максимизирована. в Qt, В2………. дь в качестве параметра Определите местоположение системы. Как и U, предположим, что в положении равновесия он равен нулю.
Положение равновесия является стабильным, поэтому, если система отклоняется от положения равновесия и находится на своем собственном устройстве, параметр qv q2 используется в течение всего времени движения. , KS и его производные остаются очень маленькими. Рассмотрим все эти величины как малые первичные величины. Полная кинетическая энергия является 2 й однородной функцией всех q. Каждый из коэффициентов Ac является функцией параметра Q. Если все эти параметры равны нулю, то они изменяются на wu. Таким образом, вы можете написать: Р = 2…. М У = Л. 2….. к Где T сумма малых количеств заказа на 2 й. С другой стороны, мы знаем, что ноль это максимальное значение функции U. И так оно и есть.
Это более высокий порядок, чем 2 й. Потому что знак выражения T h U определяется знаком самого низкого члена Далее, сумма, составляющая вторичный термин, должна остаться Перманентно положительный в обоих выражениях T и U знак выражения U не заключен в скобки. Аппроксимация заключается в удалении членов Ut и уравнения Лагранжа д ДТ ДТ ДТС ДТ ок, я ок, ок Тогда возьмите форму + + Х = М + + М с V = 1. 2…. к. Полученное K связанное дифференциальное уравнение является линейным 2D уравнением с постоянным коэффициентом. Вы можете интегрировать его, установив = со р п р….. = Х со р + р. 8 Эти значения, в случае уравнения, удовлетворяют уравнению Лагранжа. Н + гр = 0 r41 + 2 riak2 T Г2ам = 0.
Чтобы все X не были равны нулю, определитель этих линейных однородных уравнений должен быть равен нулю: 6c 6i ha ac … БЛК е АЛК я = 9 6 1 Г2ЫИ6 2 число 2 2… 6 число I Это уравнение, которое считается уравнением для чисел, определяет для этого неизвестного значения k В общем случае, а для неизвестного r 2 е попарно равное значение значения знака. Однако, поскольку решение 8 не изменяется при изменении знака r и p , r всегда считается положительным.
Смотрите также:
Теоретическая механика — задачи с решением и примерами
Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.

