Оглавление:
Задача №1.2.13.
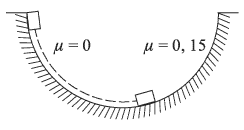
Маленькое тело соскальзывает без начальной скорости по внутренней поверхности полусферы с высоты, равной ее радиусу. Одна половина полусферы абсолютно гладкая, а другая — шероховатая, причем на этой половине коэффициент трения между телом и поверхностью 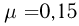 . Определить ускорение
. Определить ускорение 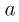 тела в тот момент, как только оно перейдет на шероховатую поверхность. Ускорение свободного падения
тела в тот момент, как только оно перейдет на шероховатую поверхность. Ускорение свободного падения 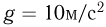 .
.
Решение:
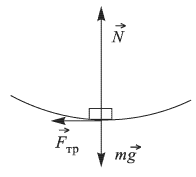
Силы, действующие на тело в момент, когда оно оказывается на шероховатой поверхности, изображены на рисунке, где введены следующие обозначения: 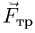 — сила трения,
— сила трения, 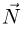 — нормальная к поверхности полусферы сила реакции,
— нормальная к поверхности полусферы сила реакции, 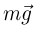 — сила тяжести. В соответствии с этим, полное ускорение тела
— сила тяжести. В соответствии с этим, полное ускорение тела 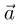 удобно разложить на две составляющие: касательную к поверхности
удобно разложить на две составляющие: касательную к поверхности 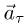 и нормальную к поверхности
и нормальную к поверхности 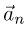 . Тогда величина ускорения тела выразится как
. Тогда величина ускорения тела выразится как 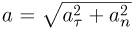 . Записывая уравнения движения тела в проекциях на касательное и нормальное к поверхности полусферы направления, имеем в рассматриваемый момент времени:
. Записывая уравнения движения тела в проекциях на касательное и нормальное к поверхности полусферы направления, имеем в рассматриваемый момент времени:
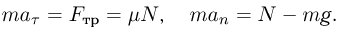
Учитывая, что 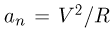 , где
, где 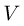 — скорость тела, из последнего уравнения находим:
— скорость тела, из последнего уравнения находим: 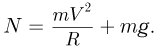 Для определения скорости тела в нижней точке полусферы воспользуемся законом сохранения энергии
Для определения скорости тела в нижней точке полусферы воспользуемся законом сохранения энергии
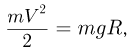
который справедлив при движении тела по гладкой поверхности. Объединяя записанные соотношения, находим:
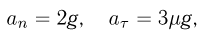
откуда следует ответ: 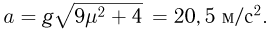
Заметим, что полученный результат позволяет также легко найти угол 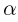 , который образует ускорение тела с вертикалью в рассматриваемый момент времени. В самом деле,
, который образует ускорение тела с вертикалью в рассматриваемый момент времени. В самом деле,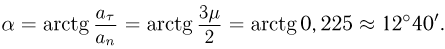
Эти задачи взяты со страницы решения задач по физической механике:
Решение задач по физической механике
Возможно эти задачи вам будут полезны:

