Оглавление:




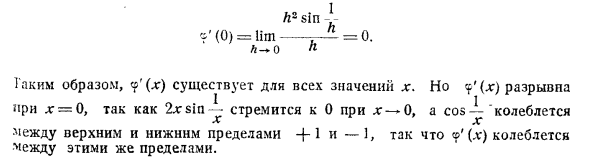

Максимумы и минимумы
- Лучший и самый низкий. Они говорят η = имеет, 9 (E) есть x =. Если оно близко к другим значениям, полученным с помощью 9 (4 когда — и когда; <:: —. Минимальное значение также определено Точка A соответствует максимальному значению, а точка B соответствует минимальному значению функции 36. Тот факт, что Л3 соответствует максимальному и минимальному значениям, заключается в том, что значение функции / больше значения Au. Обратите внимание, что это полностью согласуется с тем, что Теорема C. Предпосылкой для максимума или минимума дифференцируемой функции φ (q 🙂 является σ (Å) = 0.
Это немедленно следует из теоремы А. . Следовательно, если v = 3m3, φ = (0) = 3jc? И исчезает, когда * = 0. jc = 0 не дает ни максимума x3, ни минимума x3, которые можно увидеть на графике этой функции (рис. 9, стр. 53) Та же фигура. 36 Но 9 (5) равно 9 ‘(5) = 0 и 9’0 для всех значений x, меньших i, но все x больше 9’ (г) <^ 0-i Если оно близко к значению, оно будет максимальным, но если оно близко к A, если существует неравенство, противоположное двум последним, 9 (5) будет минимальным.
Отсутствие условий можно увидеть, рассмотрев точку C на рисунке 36 Людмила Фирмаль
Таким образом, вы можете найти интервалы (e, 5), где 9 (*) увеличивается с увеличением x (в результате 1 пункта 122) и те интервалы (£), которые уменьшаются с увеличением x. , Результат может быть сформулирован следующим образом: o ‘(a 🙂 меняет знак с положительного на отрицательный с x = Z, 9 (-c) изменяется при изменении знака 9’ (x) Будет самым большим В обратном направлении 9 (LG) является наименьшим. Максимальное значение, определенное выше, является максимальным значением в строгом смысле :: (£)>? (X) Можем ли мы потребовать, чтобы все x, близкие к 6, были слабо определены и удовлетворяли только неравенству? (5) ^? В этом определении для всех x, близких к (x), константа имеет максимальное (и минимальное) значение каждого значения переменной, например.
Теорема С все еще применима. Высокие и низкие значения иногда называют экстремальными значениями -1 -1. xВы также можете указать другие условия существования максимальных и минимальных значений. Это часто полезно. Предположим, что r (x) имеет вторую производную 9 «(). Конечно, существование ), которое вообще не следует из существования Однако в большинстве случаев, которые должны быть рассмотрены, функция имеет вторую производную.
| Трансцендентные функции | Теорема о среднем |
| Некоторые общие теоремы, относящиеся к производным | Интегрирование |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Теорема D. Если 9 ‘(5) = 0 и 9M (&) = £ 0, максимальное или минимальное значение 9 (jc) является более точным, чем jc =, максимальное значение равно 9 «($) <[0g и Минимальное значение, 9 («($)> ° — Например, 9 ‘() по теореме А Положительный для q. Достаточно маленький, чтобы быть близко, отрицательный, если x достаточно близко, чтобы быть большим. Следовательно, 9 (jc), где x = i, имеет максимальное значение. Производная всех условий, которые удовлетворяют Та же фигура. 37 С ‘(дг). непрерывно В частности, мы не функция. в связи 125. Предполагается, что < (x) имеет значение x в рассматриваемом интервале. Если это нарушается, теорема становится недействительной.
Следовательно, теорема B неверна для функций. v = 1-VX, Где квадратный корень получен со знаком плюс. График этой функции показан на фиг. 37. Здесь cp (-1) = 0, <p (1) = 0, но, как видно из чертежа, ® ‘(x) равно 1 для отрицательного x и положительного x Случай -1 и никогда не исчезает. Если x = 0, то в точке P. нет производной и нет касательной к графу. Но ясно ли, что существует максимум, если .v = 0? (Г), но достаточные максимальные условия не применяются. Предполагая только существование? ‘(X) само по себе r, возникает следующий интересный вопрос: возможна ли функция? (. *)
Имеет ли производная всех значений x, не является ли это непрерывной функцией? Людмила Фирмаль
Другими словами, кривая может иметь касательную в каждой точке, но направление касательной постоянно меняется? Интуиция, кажется, предлагает отрицательный ответ. Однако нетрудно показать, что это не так. Рассмотрим функцию, определяемую отношением e (x) = jc2sin -v, Если t <c (0) = 0, ® (g *) непрерывна для всех значений a *. Если n = ± 0, c ‘(x) = 2x sin —— cos-, Х х время L2 грех -] — (0) = Um- = 0. л — л л Следовательно, » (- *) существует для всех значений x. Но ^ ‘(х) Когда mt = 0, 2xsin имеет тенденцию быть 0, когда dm-0 и cos- X дг Между верхним и нижним пределами — {- 1 и -1. Следовательно, <p ‘(g) изменяется в одинаковых пределах.
По сути, этот же пример служит иллюстрацией проблемы, поднятой в конце пункта 122. c (l ) = -V2 sin — f-ah, X Где 0 0 и (0) = 0. Тогда o ‘(0) = a> 0. Следовательно, условие §122 теоремы A выполнено. Однако, если η> 0, o ‘(dg) = 2dg sin —- cos — f- a, X л Это уравнение варьируется между пределами x-0 a-] и a-f-l. Поскольку a-1 <0, вы можете найти значение для x, произвольно близкое к нулю. Следовательно, интервал, включающий π = 0, отсутствует. В этом случае cp (q) является строго возрастающей функцией от x. Тем не менее, *) Так называемые «простые» разрывы не могут быть даны (Глава V, пример XXXV1I.18). + 0, о ‘(х) — x ^ -0 и φ ‘(0) = c, тогда a-b = c и y’ (x) непрерывны с q = 0. См. §126 пример XLVII для доказательства. 5.

