Оглавление:








Магнито-тормозное излучение
- Магнито-тормозное излучение. Рассмотрим эмиссию заряда, движущегося в любом направлении. Периферийная скорость в постоянном однородном магнитном поле, такое излучение называется магнитным тормозом.
Радиус орбиты r и периодическая частота движения ионов выражаются формулами напряженности электрического поля H и скорости частицы v (см. § 21). г = eNu / 1-v2 / s 2 ’ V EH L V SHN = -r = -t-s -1V / 1 —— s2 • (74,1) Общая интенсивность излучения во всех направлениях определяется по уравнению (73.7).
что полная интенсивность пропорциональна квадрату импульса частиц Людмила Фирмаль
В уравнении (73.7) E = O И H _L v: 1 = 2e H v Zs s (1-v / s) (74,2) Вы можете видеть, . Если вас интересует угловое распределение излучения, вам следует использовать уравнение (73.11). Что интересно, это интенсивность, усредненная за период путешествия. Итак, интегрируем по времени вращения частицы по окружности (73.11) и делим результат на период. T = 27 г / с Ufj.
Выберите плоскость орбиты в качестве плоскости xy (начало координат находится в центре круга) и плоскость Кость yz рисуется в направлении излучения (рис. 16). Магнитное поле направлено в отрицательном направлении Направление оси z (направление движения частиц, показанное на рис. 16, соответствует положительному заряду e).
- Кроме того, b — это угол между радиальным направлением k и осью y, а <p = cujjt — это угол Между радиусом-вектором частицы и осью х. Затем косинус угла между направлением k и скоростью v равен cos cos ip (вектор v находится в плоскости xy и перпендикулярен вектору радиуса частицы в каждый момент времени). Ускорение частицы w представлено полем H и скоростью v согласно уравнению движения.
После простого расчета 27G 1T 7 e4H2v2 (l v2 h [(1-v2 / c2) sin2 0 + (v / c-cos ^ cos 7 dl = do — 9 9, (1 —- = ■) / ———, -L— /, h ‘——- z ——- —dip 8tg ts s J (1- (v / c) от cos до ip) о (74,3) (Интеграл по времени равен dip = = cujjdt). Процесс интеграции является базовым, но расчет Это довольно громоздко. Результат e4H2v2 (l- ^ r) [2-cos2 0- (l + ~ 2 ~ S) cos4 # 1 TT 7 V s2 / L 4s2 V s2 J \ dl = do ——- —————————————- -37т ——-. (74,4) Stt t s (1_ (v2 / s2) cos2c) 1
но скорость По мере приближения к скорости света он становится очень большим Людмила Фирмаль
Отношение интенсивности излучения под углом в = 7 г / 2 (Перпендикулярно плоскости орбиты) и угол b = O Равен (в плоскости орбиты) (Di / do) o _ 4 + 3r> 2 / s 2 (Di / do) * / 2 8 (1-v2 / c2f ‘2 * (74,5) Когда v- »0, это отношение имеет тенденцию быть 1/2, . Вернитесь к этому вопросу ниже.
Далее рассмотрим спектральное распределение излучения. Поскольку движение заряда является периодическим, мы будем говорить о разложении рядов Фурье. Удобно начать расчет с использованием векторного потенциала. Существует выражение для компонента Фурье (ср. (66.12)) eikR0 G A n-e j) exp {i (wHnt-kr)} dr, Где интегрирование выполняется вдоль пути частицы (Круг). Для координат частиц x = rcosuoHt, Y = = r
Выберите угол ip = ooiit в качестве интегральной переменной sin. Заметили kr = sin cos (p = -in cos (p и (, K = pion / c = nvjcr), найти компонент Фурье Векторный потенциал 2р ^ A-ev JkRo ■ ХП-〜С 2ttcR o о J exp rn {^ p — cos in sin <p ^ sin ip dip. Нам пришлось иметь дело с такой интеграцией уже в §70. Он представлен производной функции Бесселя: Axn = ~% eikRoj’n ^ cose) — (74-6) Аналогично, Aup рассчитывается как: -A-Gb-uppp, —but cos -eikRoJn (™ cosey (74,7) Очевидно, что вдоль оси z нет компонентов.
Согласно формуле §66, С элементом телесного угла co = pion: dln = f | Hn | 2 do = f | [kA „] | 2R02do. Z7T Z7T Заметили [Ak] | 2 = A2k2 + A2k2 sin2 0, Подставляя уравнения (74.6) и (74.7), получаем следующее уравнение для интенсивности излучения (Г. А. Шотт, 1912). n2e4Ya 2 Вы. = (’■ 7) [tg2е ‘J“ (т008 «) + 7 J» (т008е) (74,8) Чтобы определить общую интенсивность излучения для частоты ω = pion во всех направлениях, это уравнение должно быть интегрировано под всеми углами.
Тем не менее, он не может быть интегрирован в окончательной форме. Через серию преобразований, используя несколько теоретических отношений Функция Бесселя, желаемая интеграция Следующий формат: V / C , _2е4Я2 n m2c2v о (74,9) Рассмотрим гиперрелятивистский случай более подробно. Когда скорость частиц близка к скорости света.
Вставка числителя формулы (74.2) v = c, Общая интенсивность магнитного тормозного излучения в гиперрелятивистском случае пропорциональна квадрату энергии частицы 2е4Я2 / ё \ 2 Угловое распределение излучения в этом случае очень велико Zotoropikku. Он в основном сосредоточен вблизи поверхности трека. Угловая ширина D0, основная часть Yaivolsu z и ytine tso okgel, yayne chulzi1 y2 2 l 1 y21 — cos and ~ 1—. в
Очевидно, что = ^ (74.11) (Конечно, этот результат следует угловому распределению мгновенной интенсивности, обсужденному в предыдущем разделе (см. (73.12) x)). Это супер-релятивистский и имеет конкретную личность Спектральное распределение излучения также (Ю. И. Арцимович и И. Я. Померанчук, 1945).
В этом случае основная роль излучения заключается в следующем Воспроизвести очень большую частоту n. В этом контексте можно использовать асимптотическую формулу (70,9). J 2n (2 <) <-Φ [n 2/3 (1-Ј2)]. (74.12) y / 7G77 / Подстановка этого уравнения в (74.9) дает следующее уравнение для общего спектрального распределения излучения. / n = 2e N P о Vn-Φ ‘(u) -> JΦ (u) du, (74.13) = «2 / с / Если u = 0, выражение в квадратных скобках Постоянный предел -Ф ‘(0) = 0,4587 … 3).
Следовательно, w <1 У нас есть / „= 0.52 1″ n «(L) ‘- (74,14) t s \ <5 / V t s J Для и 1, вы можете использовать хорошо известное асимптотическое поведение Формула функции Эйри (см. Примечание на стр. 210) и Для того, чтобы получить Te4H2n1 / 2 / mc2 \ 5/2 2 2 (mc2 \ rA ^ / Ј \ 3 = ^ Ыexp expЛ-> b n >> w) • (74,15) То есть при очень большом n интенсивность уменьшается экспоненциально.
Поэтому спектральное распределение является максимальным при n rsj (S / m c2) 3, и большая часть излучения сосредоточена в диапазоне частот. А; = и, я (А) 3 = — (А) ‘- (74,16) \ t s / t s \ t s / Эти частоты очень велики по сравнению с расстоянием между Запустите две смежные вещи. Другими словами, спектр излучения состоит из большого числа плотных линий, Другими словами, он имеет квазинепрерывные характеристики.
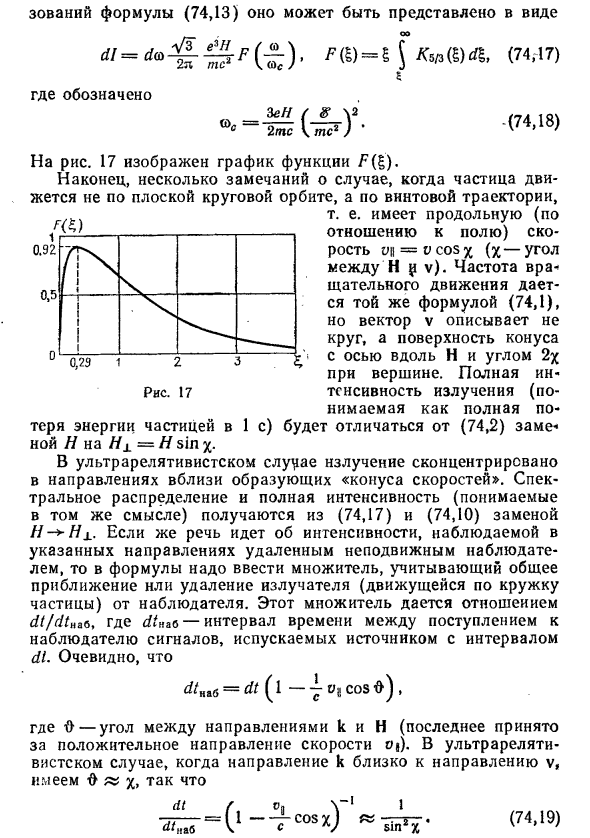
Таким образом, вместо функции распределения 1n, ряд последовательных частот oo = pion? Вы можете ввести распределение в Письменно дл = индн = в да Полезно выразить это распределение в численных расчетах Через функцию Макдональда K »1). Простое преобразование уравнения (74.13) можно выразить как: сы d l = t = (<7417>
Расположение показано 3 эГ 00 C = —— I 2tf \ tf ~ На фиг.17 показан график функции F (^). Наконец, несколько предостережений, когда частицы движутся по спиральной траектории, а не по плоской круговой траектории, то есть когда они имеют вертикальную скорость (относительно поля) r> q = vcosx (x — угол между f H и V).
Скорость вращения одинакова Уравнение (74.1), где вектор v не является кругом, Конус с углом 2% на оси и вершиной вдоль H. Общая интенсивность излучения (понимается как полная потеря энергии частиц в секунду) Он отличается от (74.2) заменой H на H ± = H sin%. Если гиперрелятивистский, радиация сосредоточена По направлению к генератору «конус скорости».
Спектральное распределение и полная интенсивность (В том же смысле) из (74.17) и (74.10) H- » -> ■ H ±. Если удаленный фиксированный наблюдатель говорит об интенсивности, наблюдаемой в этих направлениях, формула должна вводить фактор, который учитывает общее приближение или удаление излучателя (движется по кругу) Частицы) от наблюдателя.
Этот фактор dt / c ^ nabe, где GDe ^ nab — интервал времени между поступлением сигналов от источника с интервалом dt наблюдателю. Очевидно, что dtHaЈ = d t (l- \ i \\ cos ??), Где d — угол между направлениями k и H (последнее считается положительным направлением скорости u).
В гиперрелятивистском случае, когда направление близко к направлению v, Потому что есть $ ~ x TD-1 dtnafa (L- ^ c o s x) sin2 x ‘(74.19) Задача 1. Определить закон изменения энергии зарядки с течением времени. Он движется по круговой орбите в однородном магнитном поле и теряет энергию из-за излучения.
Решения. Согласно (74.2) потери энергии в единицу времени следующие. AS2е4Я22 2 4ч —— = ——— мф) дт 3 т с (Энергия S´-частицы). Найти здесь / 2e4H2 \ cth (—g-pt + const). При увеличении t энергия монотонно уменьшается, значение 8 = = Асимптотически при mc2 (полная остановка частиц) до. 2. Если частица движется по кругу со скоростью, не близкой к скорости света, найдите асимптотическое выражение для спектрального распределения излучения с большим значением n.
Решения. Используйте известные формулы для теории функций Бесселя. Мс) = Действительно 1 для n (1-s2) 3/2. С этой помощью (74,9) 2 ^ T_eAN2y / n (l v2 ^ 5/4 я n-_ „4 1 2J v / c //, V2 Это уравнение может быть применено к n (1-v2 / c2) 3 ^ 2 1. Если кроме 1 -v2 / s2 Если оно меньше, формула (74.15). 3. Найти поляризацию магнитного тормозного излучения.
Решения. Электрическое поле Ep выражается векторным потенциалом A p (74,6), (74,7) En = — [[kA „] k] = —-k (kA„) + ik An. Для ~ Пусть ei и B2 единичные векторы в плоскости, перпендикулярной к, Где ei параллельна оси x, а e2 находится в плоскости yz (эти компоненты: ei = (1, 0, 0), B2 = (0, sin #, -cos #)), векторы ei, b2, k образуют правильную тройку.
Электрическое поле работает следующим образом. E77, -ikAxnei And-ik sin 0 AuP © 2, Или опустите общие факторы, которые не важны. Enco-Jn (j-c o s ^ e i + tg6Jn co s ^ z e2- Волны эллиптически поляризованы (см. § 48). Суперрелятивистский случай для больших и малых углов в функциях Уравнения Jn и J’n выражаются в случае 1/3 и K2 / 3 i и с заданными аргументами.
В результате En = erpK2 / 3 (^ 3) + d * BK1 / a (^ 3), Φ = f Y + # 2- При 9 = 0 эллиптически поляризованный свет линейно вырождается вдоль ei. Для больших b (| 0 | mc2 / 2, pv3 1), Kr / 3 (x) ~ K2 / s (x) ~ & Y / 7r / 2x e ~ x, поляризация имеет тенденцию быть круглой. Enoo ei ± ge2; int Однако интенсивность излучения уменьшается экспоненциально.
В средней области угла малая ось эллипса проходит вдоль B2, Вдоль биг-эя. Направление вращения (в> 0, Как показано на рисунке, направления H и k находятся на разных сторонах от плоскости орбиты 16).
Смотрите также:
| Поле излучения на близких расстояниях | Торможение излучением |
| Излучение быстро движущегося заряда | Торможение излучением в релятивистском случае |

