Оглавление:
Магнитное поле — это форма материи, окружающей движущиеся электрические заряды. Магнитное поле окружает проводники с током.
Силовой характеристикой магнитного поля является магнитная индукция.
Магнитная индукция 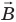 — это величина, равная отношению максимального момента силы, вращающей контур с током в магнитном поле, к силе тока в этом контуре и его площади:
— это величина, равная отношению максимального момента силы, вращающей контур с током в магнитном поле, к силе тока в этом контуре и его площади:
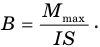
Другое определение магнитной индукции: магнитная индукция — это величина, равная отношению максимальной силы, действующей на проводник с током в магнитном поле, к силе тока в нем и длине этого проводника в магнитном поле:
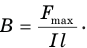
Магнитная индукция — векторная величина. Вектор магнитной индукции совпадает по направлению с положительной нормалью 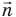 к плоскости контура. За
к плоскости контура. За
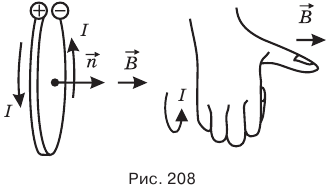
направление положительной нормали п принято направление поступательного движения правого винта (буравчика), когда его головка вращается по току в контуре (рис. 208).
Правым винтом может служить ваша правая рука. Если свернуть четыре пальца правой руки в направлении тока в контуре, то большой палец, отставленный на 90°, покажет направление положительной нормали и вектора магнитной индукции.
Единица магнитной индукции в СИ — тесла (Тл).
Магнитное поле изображают графически с помощью магнитных силовых линий или линий вектора магнитной индукции.
В природе не существует магнитных зарядов, поэтому линии вектора магнитной индукции всегда замкнуты.
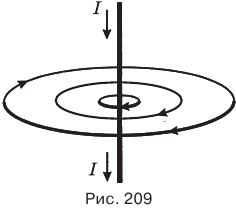
Магнитное поле является вихревым, в отличие от потенциального электростатического поля, линии которого всегда разомкнуты, т. к. начинаются и оканчиваются на электрических зарядах. Линии вектора магнитной индукции охватывают проводники с током. Линии вектора магнитной индукции поля прямого тока представляют собой концентрические окружности с центром на проводнике с током (рис. 209). Их направление можно определить с помощью правого винта (или с помощью вашей правой руки: если большой палец правой руки направить по направлению тока в проводнике, то четыре загнутых пальца покажут направление линии магнитной индукции). По мере удаления от проводника с током индукция магнитного поля этого тока уменьшается.
Магнитное поле, в каждой точке которого вектор магнитной индукции одинаков, называется однородным. Линии магнитной индукции однородного поля представляют собой прямые, расположенные на одинаковом расстоянии друг от друга. Чем гуще они располагаются, тем больше магнитная индукция.
Примером однородного магнитного поля является магнитное поле внутри длинного соленоида — катушки с током (рис. 210).
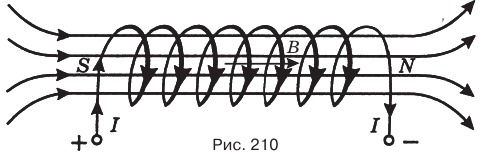
Линии магнитной индукции выходят из северного полюса N и входят в его южный полюс S.
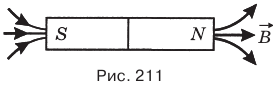
Магнитное поле полосового магнита (рис. 211) наибольшее на его полюсах, а в центре его магнитная индукция равна нулю.
Если в однородное поле внести контур с током, расположив его плоскость параллельно линиям магнитной индукции, то на стороны контура, перпендикулярным линиям магнитной индукции, будет действовать пара сил Ампера, которая создаст максимальный вращающий момент сил 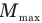 , равный произведению индукции магнитного поля, силы тока в ней и ее площади:
, равный произведению индукции магнитного поля, силы тока в ней и ее площади:
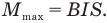
Если плоскость контура расположена под углом к линиям вектора индукции однородного магнитного поля, то момент сил определяет формула
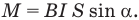
Здесь 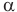 — угол между вектором индукции магнитного поля и нормалью к плоскости рамки.
— угол между вектором индукции магнитного поля и нормалью к плоскости рамки.
Момент сил, вращающих контур с током в однородном магнитном поле, равен произведению индукции этого поля, силы тока в контуре, площади контура и синуса угла между векторами магнитной индукции и нормали к плоскости контура.
Если плоскость контура перпендикулярна линиям вектора магнитной индукции, то вращающий момент сил равен 0, а силы Ампера действуют в плоскости контура, деформируя его.
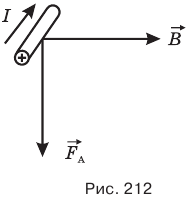
Направление силы Ампера можно определить по правилу левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в ладонь, а четыре вытянутых пальца направить по току в проводнике, то большой палец, отставленный на 90 , покажет направление силы Ампера, действующей на этот проводник в данном магнитном поле (рис. 212).
Если проводник с током расположить параллельно магнитным линиям, то сила Ампера на него действовать не будет.
Сила Ампера
Величину силы Ампера определяет закон Ампера: сила F, действующая на проводник с током в однородном магнитном поле, равна произведению магнитной индукции этого поля В, силы тока в проводнике I, длины проводника в магнитном поле I и синуса угла а между направлением магнитного поля и направлением тока в проводнике:
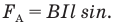
Сила, с которой магнитное поле действует на движущийся в нем заряд, называется силой Лоренца.
Сила Лоренца
Сила Лоренца 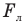 действующая на заряд q, движущийся в однородном магнитном поле, равна произведению индукции этого поля В на заряд, на скорость его движения v и на синус угла
действующая на заряд q, движущийся в однородном магнитном поле, равна произведению индукции этого поля В на заряд, на скорость его движения v и на синус угла 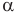 между направлением магнитного поля и направлением движения заряда
между направлением магнитного поля и направлением движения заряда
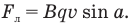
Определить направление силы Лоренца можно тоже по правилу левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления движения отрицательного заряда), то большой палец, отставленный на 90″, покажет направление силы Лоренца.
Заряженная частица, влетевшая в однородное магнитное поле перпендикулярно его магнитным линиям, движется равномерно по окружности, охватывающей магнитные линии.
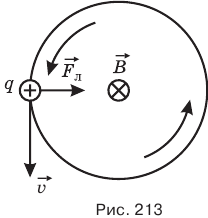
При этом сила Лоренца направлена по радиусу к центру окружности.
На рис. 213 положительно заряженная частица с зарядом q, влетевшая в направлении, показанном вектором v в однородное магнитное поле индукцией В, направленном за чертеж, движется вокруг магнитных линий против часовой стрелки.
Если заряженная частица влетает в магнитное поле под углом к магнитным линиям, то она станет двигаться по винтовой линии (рис. 214), вращаясь по окружности с линейной скоростью, равной нормальной составляющей 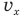 вектора скорости usin а, и одновременно перемещаясь
вектора скорости usin а, и одновременно перемещаясь
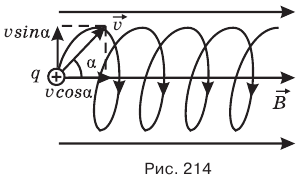
равномерно вдоль линий вектора индукции магнитного поля с тангенциальной составляющей vcos а вектора скорости 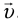 .
.
Расстояние х, которое она пролетит вдоль магнитной линии за один оборот, называется шагом винта. Поскольку вдоль магнитной линии частица движется с постоянной скоростью и, то шаг винта равен
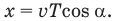
Здесь Т — период, т.е. время одного оборота частицы вокруг магнитных линий.
Сила Лоренца всегда перпендикулярна вектору скорости и, следовательно, вектору перемещения заряда, поэтому она работы перемещения заряда в магнитном поле не совершает, вследствие чего кинетическая энергия заряда, движущегося в магнитном поле под действием силы Лоренца, не изменяется.
Если заряженная частица движется одновременно в электрическом и магнитном полях (т.е. в электромагнитном поле), то на нее действует обобщенная сила Лоренца, равная векторной сумме силы Лоренца, действующей на нее со стороны магнитного поля, и силы Кулона, действующей со стороны электрического поля.
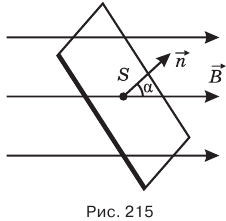
Пусть в однородном магнитном поле индукцией находится некоторая площадка S (рис. 215).
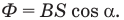
Магнитный поток Ф, создаваемый однородным магнитным полем сквозь некоторую площадку, равен произведению индукции этого магнитного поля В на величину площадки S и на косинус угла а между вектором магнитной индукции и нормалью 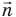 к площадке.
к площадке.
Если площадка S расположена перпендикулярно магнитным линиям однородного поля, то магнитный поток, пересекающий ее, максимален:
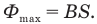
Если площадка S расположена параллельно магнитным линиям, то они ее не пересекают, поэтому магнитный поток через площадку в этом случае равен нулю.
Магнитный поток
Магнитный поток — скалярная алгебраическая величина, т.е. он может быть положителен и отрицателен, поскольку косинус угла может быть больше и меньше нуля.
Если магнитный поток пересекает замкнутую поверхность (представьте ее в виде надутого воздушного шарика), то, поскольку все магнитные линии непрерывны и замыкаются сами на себя, число входящих в эту поверхность магнитных линий, создающих отрицательный поток, будет равно числу выходящих магнитных линий, создающих численно такой же по модулю, но положительный поток. Поэтому полный поток вектора магнитной индукции сквозь замкнутую поверхность равен нулю. Это важное свойство магнитного поля свидетельствует об отсутствии в природе магнитных зарядов и вихревом характере магнитного поля.
Единица магнитного потока в СИ — вебер (Вб).
Когда магнитный поток сквозь площадь, ограниченную проводящим контуром, изменяется, в этом контуре возникает индукционный ток.
Правило Ленца: индукционный ток всегда направлен так, что своим магнитным полем он противодействует изменению магнитного потока, вызвавшего этот ток.
Обратимся к рис. 216, а). Когда магнитный поток сквозь контур, создаваемый внешним по отношению к контуру магнитным полем индукцией 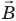 , нарастает
, нарастает 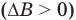 , индукционный ток
, индукционный ток 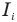 в контуре направлен так, что его магнитное поле индукцией
в контуре направлен так, что его магнитное поле индукцией 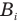 (на рис. 216, а) оно изображено штриховыми стрелками), антинаправлено внешнему магнитному полю, противодействуя увеличению магнитного потока. Отметим, что направление тока
(на рис. 216, а) оно изображено штриховыми стрелками), антинаправлено внешнему магнитному полю, противодействуя увеличению магнитного потока. Отметим, что направление тока 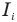 связано с направлением своего магнитного поля
связано с направлением своего магнитного поля 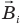 правилом правого винта — буравчика. Когда же магнитный поток, создаваемый внешним магнитным полем индукцией
правилом правого винта — буравчика. Когда же магнитный поток, создаваемый внешним магнитным полем индукцией  убывает (рис. 216, б), индукционный ток в контуре изменяет свое направление на противоположное и при этом его магнитное поле
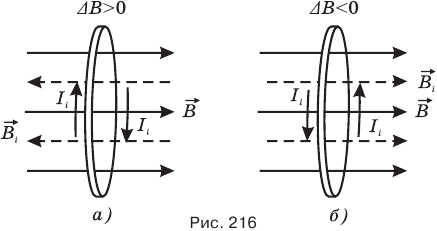
убывает (рис. 216, б), индукционный ток в контуре изменяет свое направление на противоположное и при этом его магнитное поле 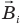 оказывается сонаправленным с внешним полем
оказывается сонаправленным с внешним полем  . Теперь магнитное поле индукционного тока противодействует убыли магнитного потока, создаваемого внешним магнитным полем сквозь контур, поддерживая его.
. Теперь магнитное поле индукционного тока противодействует убыли магнитного потока, создаваемого внешним магнитным полем сквозь контур, поддерживая его.
Явление возникновения индукционного тока в контуре при изменении магнитного потока, пересекающего этот контур, называется электромагнитной индукцией. По закону Ома сила индукционного тока 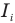
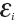 прямо пропорциональна ЭДС индукции и обратно пропорциональна сопротивлению контура В:
прямо пропорциональна ЭДС индукции и обратно пропорциональна сопротивлению контура В:
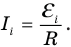
Закон Фарадея
Закон Фарадея для электромагнитной индукции: ЭДС электромагнитной индукции, возникающая в контуре при всяком изменении магнитного потока, пересекающего этот контур, равна скорости изменения магнитного потока, взятой со знаком минус,
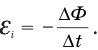
Здесь 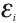 — ЭДС индукции в контуре,
— ЭДС индукции в контуре, 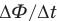 — скорость изменения магнитного потока, пересекающего контур, N — число витков в контуре (безразмерное).
— скорость изменения магнитного потока, пересекающего контур, N — число витков в контуре (безразмерное).
Эта формула справедлива, когда магнитный поток изменяется монотонно, т.е. когда за равные промежутки времени 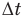 он изменяется на одинаковую величину
он изменяется на одинаковую величину 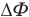 и ЭДС индукции постоянна. Если же магнитный поток изменяется произвольно, то увеличиваясь, то уменьшаясь, что бывает при вращении контура в магнитном поле, то пользоваться этой формулой для определения мгновенного значения ЭДС индукции нельзя, по ней можно определить только среднее значение ЭДС индукции.
и ЭДС индукции постоянна. Если же магнитный поток изменяется произвольно, то увеличиваясь, то уменьшаясь, что бывает при вращении контура в магнитном поле, то пользоваться этой формулой для определения мгновенного значения ЭДС индукции нельзя, по ней можно определить только среднее значение ЭДС индукции.
При произвольном изменении магнитного потока сквозь контур ЭДС индукции равна первой производной магнитного потока по времени, взятой со знаком минус:
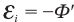
Здесь 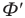 — первая производная магнитного потока по времени.
— первая производная магнитного потока по времени.
Знак минус в этих формулах объясняется правилом Ленца.
Если контур, пересекаемый переменным магнитным потоком, содержит не один, а N витков, то ЭДС индукции в нем будет в N раз больше, чем в одном витке. При этом предыдущие формулы примут вид:
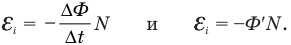
ЭДС индукции, возникающая в проводнике, движущемся поступательно в однородном магнитном поле под углом к магнитным линиям, равна произведению индукции этого поля на скорость проводника, на его длину в этом поле и на синус угла между вектором индукции магнитного и вектором скорости проводника:
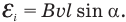
ЭДС индукции 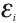 , возникающая в контуре, вращающемся равномерно в однородном магнитном поле, равна произведению угловой скорости
, возникающая в контуре, вращающемся равномерно в однородном магнитном поле, равна произведению угловой скорости 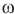 контура на индукцию В магнитного поля, на площадь контура S и на синус угла а между вектором магнитной индукции и нормалью к плоскости контура:
контура на индукцию В магнитного поля, на площадь контура S и на синус угла а между вектором магнитной индукции и нормалью к плоскости контура:
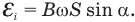
В случае, когда плоскость контура параллельна магнитным линиям, угол 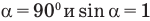 . Тогда ЭДС индукции в контуре будет максимальна.
. Тогда ЭДС индукции в контуре будет максимальна.
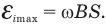
Если контур содержит N витков, то ЭДС индукции в нем в N раз больше, чем в одном витке:
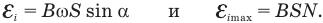
Явление возникновения ЭДС индукции и индукционного тока в контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции.
Магнитный поток Ф сквозь катушку (или контур любой иной формы) прямо пропорционален силе тока в ней, т.е. между этими величинами существует прямо пропорциональная зависимость:
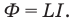
Здесь L — коэффициент пропорциональности между током и связанным с ним магнитным потоком. Он называется коэффициентом самоиндукции контура или его индуктивностью. Величина индуктивности зависит от формы и размеров самого контура, а также от магнитных свойств среды, и постоянна для данного контура. Индуктивность контура — скалярная положительная величина. Она не зависит от наличия или отсутствия тока в нем. Индуктивность катушек заводского изготовления указывается в их паспорте.
Единица индуктивности в СИ — генри (Гн).
ЭДС самоиндукции 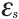 , возникающая в контуре при изменении тока в нем, прямо пропорциональна скорости изменения силы тока в контуре, взятой со знаком «минус»:
, возникающая в контуре при изменении тока в нем, прямо пропорциональна скорости изменения силы тока в контуре, взятой со знаком «минус»:
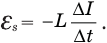
Здесь 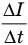 —скорость изменения силы тока, т.е. изменение силы тока за единицу времени.
—скорость изменения силы тока, т.е. изменение силы тока за единицу времени.
Если ток в контуре изменяется произвольно, то пользоваться этой формулой для определения мгновенной ЭДС самоиндукции нельзя, по ней можно определить лишь среднее значение ЭДС самоиндукции за время 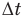 . Для определения мгновенного значения ЭДС самоиндукции в этом случае надо пользоваться формулой
. Для определения мгновенного значения ЭДС самоиндукции в этом случае надо пользоваться формулой
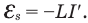
Мгновенная ЭДС самоиндукции прямо пропорциональна первой производной силы тока по времени, взятой со знаком «минус».
Магнитное поле, как и всякое силовое поле, обладает энергией.
Энергия магнитного поля катушки с током соленоида равна половине произведения индуктивности этого соленоида на квадрат силы тока в нем:
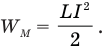
Поскольку магнитное поле размыто по пространству, то, чтобы охарактеризовать его энергетические свойства, вводят величину, равную энергии магнитного поля в единице объема пространства, занятого этим полем. Эта величина называется объемной плотностью энергии магнитного поля 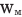 .
.
Объемная плотность энергии магнитного поля 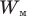 равна отношению энергии магнитного поля к объему V пространства, занятого им:
равна отношению энергии магнитного поля к объему V пространства, занятого им:
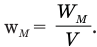
Объемная плотность энергии магнитного поля прямо пропорциональна квадрату магнитной индукции этого поля и обратно пропорциональна относительной магнитной проницаемости окружающей среды:
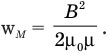
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти страницы:

