Оглавление:












Лучистый теплообмен внутри замкнутой поверхности
- Описанная ниже проблема часто встречается в технических расчетах. Контейнеры с неравномерной температурой стенок заполняются не-или выделяющимися газами. Потребность в радиации Передача тепла между различными поверхностями и газами в сосуде. Как правило, температура поверхности поддерживается при определенной температуре. Он может быть нагрет или Предполагается, что другие / поверхностные температуры изменяются адиабатически по отношению к тепловому потоку.
Топка парового котла показана на рисунке 14-15 приведены примеры таких контейнеров. Механические печи обычно покрывают слоем раскаленного угля, температура которого считается одинаковой (расчет известен, неизвестно). Температура Трубчатая поверхность котла практически совпадает с температурой водяного пара в трубе. Температура огнеупорной стенки определяется балансом тепла, полученного и выделенного излучением Конвекция.
Первые паровые машины появились во второй половине 18 века и ознаменовали наступление промышленной революции. Людмила Фирмаль
Поскольку лучистая теплопередача обычно доминирует, расчет, который игнорирует конвективную теплопередачу, является подходящим приближением. Внутренний объем Камера заполнена газом, который участвует в радиационном обмене. Расчет теплопередачи и температуры стенок и газа в сосуде является очень сложной задачей. 、 Значительные simplification. In дело в том, что температура огнестойкой стены (она отличается от точки к точке). Для расчетов эти стены обычно делятся на ограниченное количество участков. Температура считается постоянной.
Внутренняя температура и состав пламени или горючих газов в камере также изменяются от точки к точке. Point. In такой расчет, как этот Заполните пространство в камере однородным газом одинаковой температуры или разделите его на конечное число объемов, а затем отрегулируйте температуру и состав Предельные значения для каждого тома считаются постоянными. Неэмиссионный газ, черный surface. In в этом разделе мы предполагаем, что объем заполнен газами, которые не выделяют и не поглощают .
Теплый. Контейнер состоит из n стенок, поверхность которых рассеивается и отражается. Излучение следует закону косинусов, температура постоянна на каждой поверхности, коэффициент пропускания равен Внимание к тепловой конвекции не принимается. Для некоторых поверхностей задается температура, а температура других поверхностей считается изменяющейся адиабатически. Вам нужно рассчитать Лучистый теплообмен между различными поверхностями и неизвестными температурами адиабатических поверхностей.
Коэффициент угла между поверхностями равен Он также известен как»Золотой Треугольник». Во-первых, мы предполагаем, что все поверхности черные. Тогда решение будет легким. Теплообмен между 2 произвольными поверхностями/и представлен: / — Теплообмен между поверхностью и остальной частью контейнера получается суммированием: (14-24) все поверхности равного числа можно разделить на 2 группы. Первый. Так как группа знает температуру 7, то также необходимо определить тепловой поток qi. Во 2-й группе тепловой поток qi = 0, необходимо рассчитать температуру.
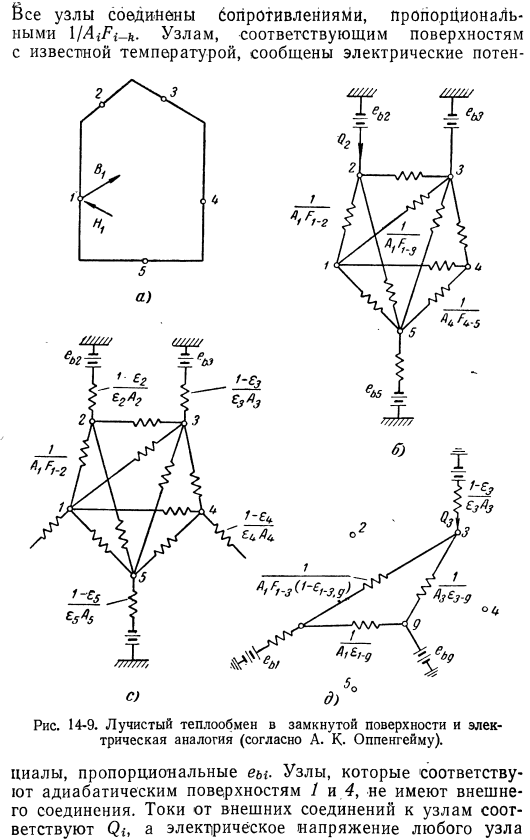
Задачи включают в себя Неизвестное число определяется путем решения линейного уравнения. В. Пашкиз, недавно А. Окей. Оппенхайм. 267]для такого процесса радиационного обмена Создайте электрическую аналогию. Рис. 14-9. 6-Схема контейнера, показанная на фиг. 1. 14-9, а; контейнер состоит из 5 поверхностей, температура поверхности 2, 3, 5 Вы можете настроить его заранее. Аналогично узел соответствует поверхности сосуда. §Все узлы соединены резистором, пропорциональным / aifi-k. Соответствующие узлы Если температура находится на известной поверхности, то потенциал сигнализируется. 14-9.
Радиационный теплообмен в замкнутом состоянии Поверхностная и электрическая аналогия (А. Оппенгейма). Отсутствуют внешние узлы для чаш и изоляционных поверхностей 1 и 4, которые пропорциональны ЭМ Соединение. Ток от внешнего подключения к узлу соответствует qf, а напряжение узла без внешнего подключения соответствует излучательной способности Соответствующая поверхность изоляции. Поэтому при применении метода электрической аналогии сосуд должен быть представлен как композиция пространства и всех его поверхностей.
Он должен быть включен в calculation. In на рисунках 14-9, чтобы не усложнять рисунок, поверхность вне плоскости рисунка не включается. Нерадиоактивный таз, серые стенки. Если поверхность сосудов не черная, то в сосудах возникают бесчисленные рефлексы, которые на первый взгляд кажется невозможным рассчитать. Но спасибо тебе Резюмируя процесс, описанный на стр. 494, эти трудности становятся непреодолимыми. Сначала рассмотрим серую поверхность (a = e). Буква b-это、 От единицы площади любой поверхности, а через h — весь поток, который попадает в единицу площади.
Выведите уравнение теплопередачи q между поверхностью i и остальной замкнутой частью Контейнер. Тепловой поток, исходящий от поверхности, представляет собой aib {. Он также может быть представлен как 2 тепловых потока k, направленных от всех поверхностей к поверхности. Сайфи-КБК. Таким образом, плоская k область i теплопередачи выражается как «kako⁴-2⁵». С другой стороны, = (14-26) исходящий тепловой поток Состоит из поверхностного/, лучистого и отраженного излучения:= + (14-27) h из последних 2 уравнений. Если вы хотите исключить2: = ar ^^. — (14-28) На поверхности можно написать 1 формулу на черной поверхности, а также 2 формулы в виде (14-25) и (14-28).
Bi, с другой стороны, является дополнительным и неизвестным. Для 2n неизвестных у нас есть 2n уравнений. Поэтому остается совместно решить систему 2n линейных уравнений. Электрическая аналогия герметичных контейнеров、 / Аналогично тому, что показано на рисунке. 14-9 доступна в игре, а ’ ootpen против серой поверхностью (рис. , М-9, стр. Как показано в Формуле (14-28), сопротивление、 Пропорциональный (1-ee / eib должен быть включен в каждую ветвь, которая соединяет устройство с внешним источником напряжения.
Рассматривая аналогию, » интересный вывод: включение Сопротивление внешней стороны узла без внешнего соединения (например, узел 4) не влияет на потенциал этого узла. Это означает, что температура изолированной стены не зависит От поверхностной поглощающей способности этой стены. Обратите внимание, что первый вывод основан на предположении, что все поверхности подвергаются равномерному воздействию По всей площади. Поэтому деление замкнутого пространства на n поверхностей должно осуществляться таким образом, чтобы правильно аппроксимировать заданное conditions. So. .Если стена, на которой происходит лучистый теплообмен, не является серой поверхностью, то необходимо выразить один цвет по формулам (14-25) и (14-28) .) .
Излучение .Общее количество тепла, теряемого поверхностью i в результате радиационного обмена, определяется интегрированием по всем длинам волн: 03 Э / = Jрасчет Для изолированных стен условие Qi = O справедливо только в общих случаях, а не в монохроматическом излучении, что делает его очень громоздким .Лучистый газ .Описанные расчеты В предыдущем разделе излучение и поглощение газов могут быть расширены, если они находятся в плотно закрытом пространстве .Опять же, стенки контейнера Закон Косинуса, и что они являются диффузно-отражающими, серыми поверхностями .
Газ, заполняющий сосуд, также учитывает серый газ (D = e) в первую очередь .Позже это состояние Вы будете charged .It также предполагается, что газы имеют одинаковую температуру и концентрацию по всему объему ограниченного пространства .Уравнение также справедливо для этих условий (14 — ^ 6) и (14-27) .Объедините эти выражения, чтобы сформировать полу-выражение: (14-29) I-выражение (14-25) изменяется, так как оно является частью излучения Газ, выпущенный с поверхности k, поглощается газом до того, как он достигнет поверхности Z .С другой стороны, газ высвобождает энергию к последней поверхности .Я думаю .Уравнение, описывающее эти физические процессы .
Лучистый поток, выходящий из поверхности k и идущий к поверхности z, является лучистым потоком, исходящим от поверхности k、 Падение на поверхность z можно выразить следующим образом: в этом уравнении ei — > g — излучательная способность, а на серой поверхности по закону Кирхгофа она равна поглощению Способность .Это значение должно быть определено для всех лучей, проходящих между поверхностью i и k .получено из уравнения (13-36) .Он генерируется только по всей полусфере, а не по пространственному углу, который определяется угловым коэффициентом Fi_ₕ .
- Лучистый поток, который испускается из газа и достигает поверхности z, является e ._ ^ — излучательная способность газа. В область i .наконец, лучистый поток, покидающий поверхность z, равен: Чистая потеря лучистого тепла поверхностью z равна O / D-U-pucked= M-E L-ebg) + 2 ^ (1-e, ._м) (Б-БК) .(14-30) чисто Потери тепла за счет газа при радиационном обмене могут быть рассчитаны по неизвестным в данной задаче параметрам по формуле• (14-29) — (14-31) .Температура, температура изолированной поверхности, потери тепла или температура газа в контейнере .
Электрическая аналогия замкнутой поверхности изображена на рисунке 14-9 а Это показано на фиг .14-9, д .Только связи между узлами/, 3, и г входят .Узел g соответствует газу, помещенному в замкнутое пространство .Необходимо установить аналогичное соединение между другими пользователями .Узел .Узел g или ’ соединен с батареей, которая дает напряжение ebg при заданной температуре газа .Или, если газ не имеет источника тепла или слива, он не подключен к батарее .В первом случае ток, протекающий от аккумулятора к узлу g, пропорционален тепловым потерям, вызванным газом .
Термодинамика возникла как эмпирическая наука об основных способах преобразования внутренней энергии тел для совершения механической работы. Людмила Фирмаль
Во 2-м случае напряжение в узле g пропорционально энергии излучения черного тела при температуре Газ .Из разреза газового излучения мы знаем, что настоящий газ сильно отличается от серого object .To рассчитать лучистый теплообмен в замкнутом объеме, заполненном Серый газ, формула (14-29) — (14-31) следует использовать для монохроматического излучения .Общая теплопотерь в этом случае является монохроматической Тепловой поток по всем wavelengths .It желательно допускать определенную степень приближения, так как этот расчет будет очень сложным .
Для этой цели помогает понятие избирательности .Серый газ (л . 268] .- При приближении к фактическому газу с помощью селективного серого весь интервал длин волн делится на 2 части .Газ поглощает и прочее-все остальное .Затем расчет первого интервала осуществляется точно так же, как и расчет серого газа-в этом интервале Поглощающая способность не зависит от длины волны .Во 2-й части процесс расчета, описанный в предыдущем пункте, применяется к нерадиантному газу .Предубеждения .
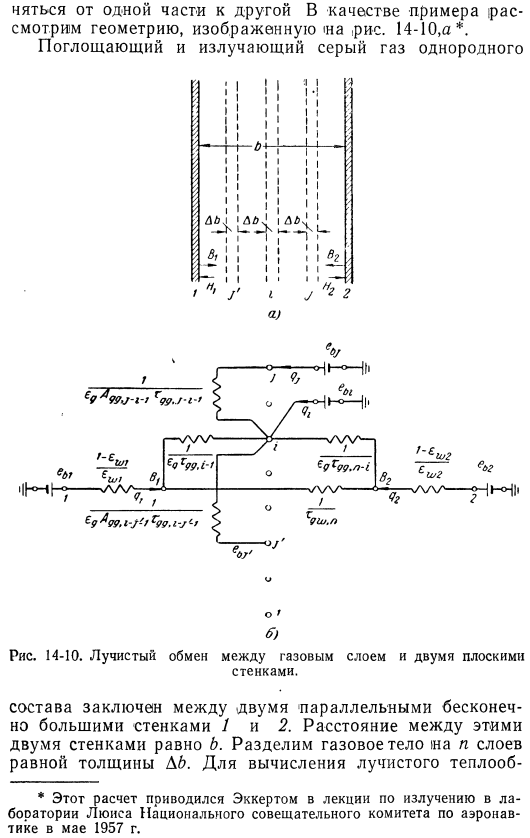
Температура газа в ограниченном пространстве z везде одинакова, и во многих случаях это нереально .Упрощение процесса расчета может быть достигнуто в следующих случаях: Газовое тело делится на множество частей, температура и концентрация которых может варьироваться от части к части .14-10, * .Равномерное поглощение и выделение серого газа 14-10 .Радиационный обмен между газовым слоем и 2 плоскими стенками .2 конфигурации параллельно Бесконечно большие стены 1 и 2 .
Расстояние между этими 2 стенками равно b .A .разделите газовое тело на N слоев равных thickness .To рассчитайте лучистое тепло*это Расчет был сделан Эккертом в 1957 году на лекции по радиации, которая состоялась в Институте Льюиса Национального консультативного совета по авиации 5 марта .Эмиссия газовых слоев и стенок, т . е .следующие величины: — полусферическая излучательная способность стенок .— Полусферическая излучательная способность газового слоя Толщина D6; k-полусферическая пропускная способность газового тела (состоящего из k слоев) к стенке излучения .
Dₖ-пропускная способность газового тела (состоит из/ г-слоя) 1 слой экструзии газа .k-поглощающая способность газового слоя толщиной b, излучение стенки при наличии ряда газовых слоев между стенками、 a Agg k, который равен k, — это поглощающая способность газового слоя к излучению другого газового слоя (обе толщины D6), а количество газовых слоев между ними равно K .эти » варианты Выбросы, а также те, которые описаны в§ 13-3, должны определяться путем интеграции .Расчет принимается во внимание, но не здесь .Поток излучения, падающий на стену/、 В этом случае можно применить уравнение (14-29) again .It осталось определить чистый убыток .
От единичной поверхности стенки 1 тепло q поступает через входящий поток от различных частей, составляющих поток, а стенка 1 попадает туда и выходит оттуда .я представляю любой слой .Получаем следующее уравнение:^ 1-+ Zg ^ gg, i — bV » = 1 это уравнение можно записать, если 2 стенки и заключенный между ними газ одинаковы .Температура .Согласно закону Кирхгофа, в замкнутом пространстве с одинаковой температурой поток излучения через любую плоскость равен.
Чистые теплопотери за счет излучения от черной поверхности и от стенки 1 равны нулю .Приведенное выше уравнение в данном случае выглядит так: 1 = n1_ Dgw . н» г] ^ г ^ гг, я — 〜* = 1• Учитывая это соотношение, предыдущее уравнение можно преобразовать следующим образом: i = n h =Dₑw, (B .-Ba)+(*>-^)-(14-32)1 = 1 соответствующее уравнение То же самое можно сказать и о стене 2 .Следующим шагом является расчет тепловых потерь, обусловленных излучением газового слоя i .Эта величина определяется излучением, испускаемым газом через оба.
Поверхности, излучающей от 2-х стенок, поток излучения поглощается в газовый слой, а излучение генерируется в 2-х газовых слояхобе стороны этого слоя и Я зацепился за него .Этот энергетический баланс может быть выражена с помощью следующей формулы:^ egebi ^ гв .Я-фигу .я — х ^1^ гв, Н-Дж = Н Дж = Н-м — ebj’ — j ’= Если применить это уравнение для той же температуры, согласно приведенным выше соображениям、 Отношение/ = 1 + s eBABg .я — ’ — ДСГ .i — i — + + s кроме того, направленная излучательная способность каждого луча равна Она будет равна указанной поглощающей способности .Поэтому Э . Д .= Д Б .Гг . б ГВт ГВт, к подставляя последние 2 уравнения в Формулу qₖ, вам.
Следующую формулу:=⁸〜+ * (ПГГ, н (е, / / =η+ с% (электронная самоуправления + / = х « б л (эй ~~ ев ^ ’ (14-33) / ’ = 1) эту задачу Опишите уравнения (14-29) и (14-32), дополненные 2 соответствующими уравнениями для стены 2 .It легко проверить, что число уравнений равно числу .(Неизвестный .Электрическая аналогия, соответствующая этим уравнениям, показана на рис .14-10 .c .вертикальный ряд узлов от 1 p соответствует номеру P слоя газа .Необходимые соединения указаны между узлом i и узлом/, 2, /, и/, respectively .By устанавливая все остальные связи таким же образом, можно создать полный контур .
Температура Различные слои газа — могут быть определены внутренним источником тепла или жарой sink .In в этом случае температуру слоя нужно считать заданной .Следовательно, напряжение узла 1_n Он установлен батареей .Лучистая теплопередача может также использоваться для определения температуры некоторых или всех газов layer .In в этом случае соответствующий узел не подключен Батарея и потенциал узла указывают на лучистую энергию черного тела, а значит и на температуру .
Для non-сернистого газа, необходимо рассчитать сначала Монохроматическое излучение и его последующее интегральное (по всем длинам волн .Этот процесс можно снова упростить благодаря концепции «избирательно серого газа» .Излучательная способность-емкость цилиндрической gap .In в предыдущем разделе свойства температуры и излучения рассматривались все ограниченные по площади и объему константы .На практике большинство параметров обычно непрерывно изменяются по рассматриваемой поверхности и объему .
Математические соображения для 3 из этих задач радиационного обмена Условие приводит к интегралу equation .As в качестве примера данного раздела рассматриваются следующие случаи: материал сверлят при постоянной температуре Цилиндрические зазоры (рис .14-11) .Стенки щели можно считать серыми, а излучательную способность материала стенки можно обозначить буквой Е .14-11 .Излучение из цилиндрического зазора .Температура стенок определяется лучистым потоком, испускаемым из любого места на поверхности щелей .
Общий поток B, который приходит из любого места Зазор будет больше, потому что излучение, отраженное поверхностью, будет добавлено к излучаемому излучению .Локальную кажущуюся излучательную способность стенки можно определить с помощью: Из следующего уравнения: поток излучения B и кажущаяся излучательная способность следует рассматривать как функцию расстояния x от края зазора .Инжекция потока излучения Единицы площади поверхности на расстоянии x обозначаются буквой N .связь между падением и разливом такой поверхности представляет собой следующую формулу: B = e ^ + (л-с) // .(14-34) для получения уравнения потока / / необходимо сначала выразить поток излучения dHy, падающего на стенку 1 из области элемента dA₂ .
Координаты, определяющие расположение AD₂ являются Y и Р . Поэтому, Dн = Б, ДФ, _₂=еа (у) edAᵢ=- ₆ (П П & 2dyDdfeaeb2ns⁴ рис .14-11 от очевидного .Соотношение: a =Deos2 (p / 2) ; s2 — [x-y) 2+£) 2cos2 (p / 2) .Если вы замените эти выражения на вышеприведенные выражения, они будут иметь следующий вид: Total flow to site、 Она определяется Интегралом по всему периметру и всей длине зазора . y = Q 9/2 = 0 выполнить интеграл по углуp, заменив x / D сквозным .И от y / D до y, это выглядит так:} 4 (4-3S) о вам нужно интегрировать раздел: y = 0 к y = x и y-x к// — oo; — — — t) / указывает, что это выражение должно быть введено как положительное .
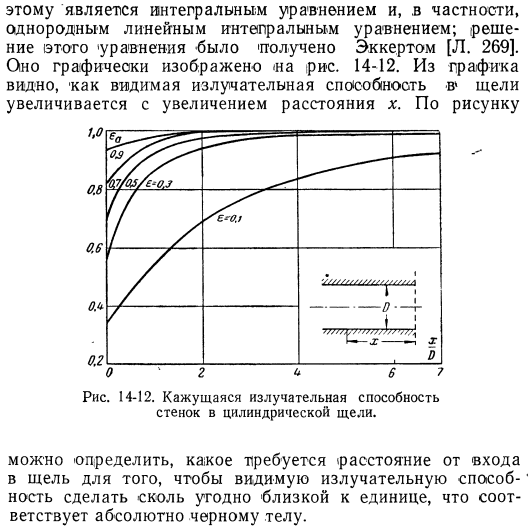
Если объединить уравнения (14-34) и (14-35), то получим:00 * Л)= «2 [(6-1)» + I) 3′ 2) 1о (14-36) неизвестный параметр ea появляется в этом уравнении .Не только фиксированное значение слева, но и значение на правой стороне интеграла .Фиксированный г |в introduction .So, формула (14-36) является интегральным уравнением, в частности однородным линейным интегральным уравнением .Решение этого уравнения является «Эккерт [L .269] .это показано на рисунке .14-12 .
Из графика видно, как видимая излучательная способность зазора увеличивается*с увеличением расстояния x .By Рис .14-12 .Видимая излучательная способность стенок внутри цилиндрического зазора .Вы можете-определить расстояние от слота Излучательная способность*может быть сколь угодно близка к единице, что соответствует абсолютно черному телу .
Смотрите также:
| Абсолютно черные тела | Лучеиспускание факела |
| Твердые, жидкие и газообразные тела | Коэффициент теплообмена при тепловом излучении |

