Локальные свойства непрерывных функций

Локальные свойства непрерывных функций

• Локальное свойство непрерывной функции. Давайте представим новую концепцию. Предположим, что функция/(x) задана множеству{D} О П Р Е Д Е Л Е Н и Е1. Функция [(x), если существует вещественный M (вещественный PG) для всех значений аргумента x

множества{x}, называется o R a n I N s V e R x y(s n I zu)для множества{x}в этом случае число M (число PG) называется множеством{x} (ИЖ N Y) gr a N О П Р Е Д Е Л Е Н и Е2.

Функция?если (x) — действительное число PG и M для всех значений аргумента x из{x}, Людмила Фирмаль

то есть{x}несмещенное неравенство/p(x) равна нулю в иррациональных точках, нулю в рациональных точках и ограничена (с обеих сторон) на любом множестве{x}. Следующая теорема о локальном пределе функции с конечным предельным значением справедлива. 4.10(Nb): a-n-n-n-n-n-n-n-n-n-n-n-n-n-n-n-n-n-n-n-n-n-n-n-n-

n-n-n-n-n-n-n-n-n-n-n-n—n-n. и существует такое положительное число 8, где функция 1 (x) является пересечением множества{x}и интервала (a-b, a+b), то есть окрестности 8 точка зрения А. З а м е ч а н и Е1. Для набора функций DX) n l o W n o K r s в некоторых B соседях точки a

• можно принять сам интервал (a-b, a+b) как/ZB. Д О К а з а т е л ь с т в о. предел^(x)в точке А равен B. Для определения предела Коши для некоторого положительного числа e, для всех значений аргумента x из проколотой точки B-OK-restnity a * неравенство / /(x) — b / 0 и отрицательны при / (a)<0. Итак, неравенство (4.28) означает, что для всех значений аргументов от точки А до точки 6 функция/(x)

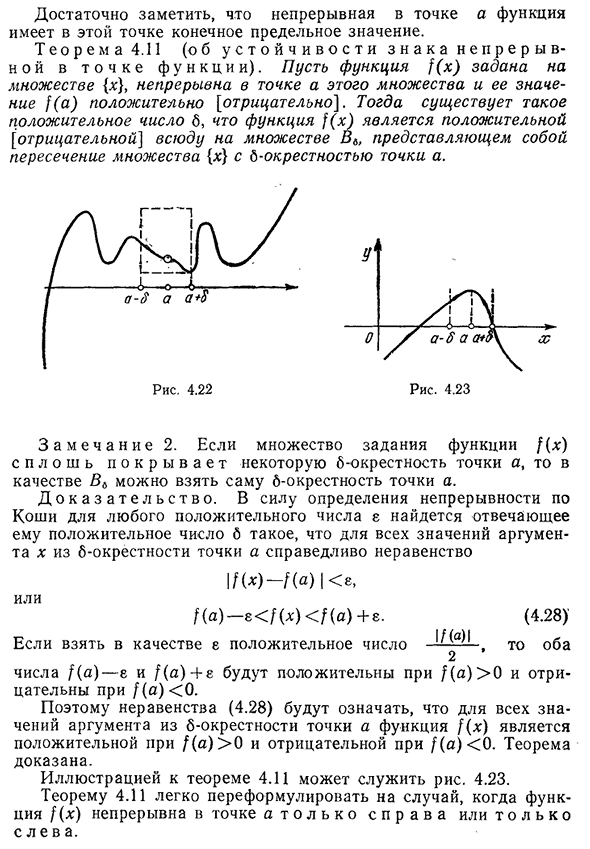
положительна при/(a)>0 и отрицательна при/(a)<0. Теорема доказана. Иллюстрацией теоремы 4.11 может служить диаграмма. 4.23 Теорема 4.11, функция/(х)является точкой » Т О Л Ь К О С П Р А В и Т О Л Ь К О С Е В в.Это легко переформулировать для дела, которые являются последовательными в».170Ч. 4. Непрерывность функций Полтора деления[а, а+б)о 6-ть semiacrest точки А П Р А В и полтора деления(а-6,а] — о-й 6-semiacrest пункта А Л Е. Т Е Р Е М А4. 11*.

Функция [(x) дана множеству { * }, смежному в точке a этого Людмила Фирмаль

множества[слева]справа, и ее значение{(a) не равно нулю. Тогда существует положительное число 6, в котором функция} (x) не исчезает, и точка a имеет тот же знак, что и точка a для всех значений x из множества{x}, принадлежащих правой[левой]6-полукругу. Чтобы доказать эту теорему, доказательство теоремы 4.11 следует повторить дословно, заменив термин «ближняя точка

b»термином»правый[левый]b-полукруг точки a». З а м е ч а н и Е3. Локальные свойства последовательных функций в данной точке зависят от доказанных выше теорем 4.1 и 4.2, непрерывности суммы, разности, произведения и частного двух последовательных функций в данной точке.

Смотрите также:

Методическое пособие по математическому анализу

Раскрытие неопределенностей других видов	Механические приложения
Вычисление числа е на ЭВМ	Формула Лейбница для n-й производной произведения двух функций.