Оглавление:

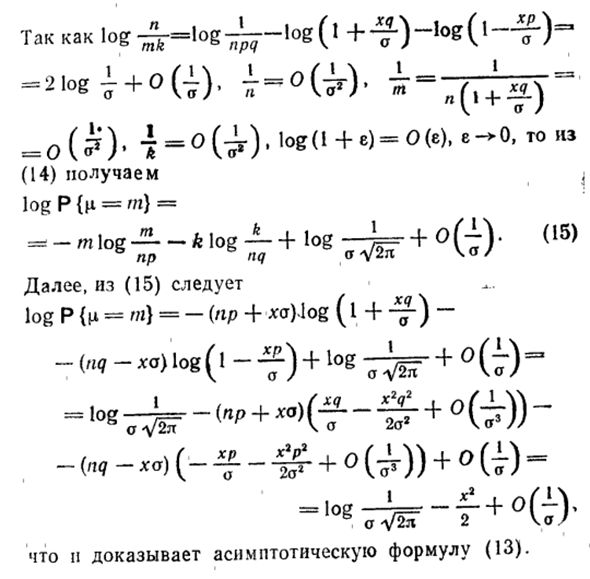

Локальная предельная теорема Муавра-Лапласа
- Локальная предельная теорема Мура-Лапласа Биномиальное распределение (1) случайной величины η имеет M ^ -pr и D \ i = npq (см. Задачу 3 в главе 3). o = l / npq выражается как стандартное отклонение.
- Доказанная ниже теорема дает асимптотическую формулу для биномиальной вероятности (I), когда p не близко к 0 или 1. Для схем Бернулли a = n / npq-> oo и C> 0 все они равномерны. м-пр x =-где m неотрицательное целое число, c- * i (1 + 0 (1)).
Теорема 3. (Локальная предельная теорема Муара-Лапласа.) Людмила Фирмаль
- (| 3) (Ynpq) Доказательство. Пусть m = pr + xo. Оценить лог вероятности равных log P {\ i = m) = log n! -log m \ -log (n-m) I + + rn log p + (n-m) log q используйте асимптотические формулы Стирлинга, такие как n-> oo log n \ = n log n + log U2yaya-l + 8L, Здесь 8 „= 0 (~), k = n-m = nq-xo, и из гипотезы теоремы m = pr (l + k = nq (i-> oo, поэтому мы можем применить формулу.
Стирлинга для оценки log!,!, log ml, log ft!: logP (q = m) = n log n-m log m-k log k + + m \ ogp + klogq + ± log1 ^ + Qn-Qm-Qk. (14) войти ^ =! Og (t + -log (1 = 1 + 0 (1). 1-оф. = 0 (?) • 4 = 0 (1-). Log (! + E) = 0 (e), e-> 0 и из (14) log P {μ = w} = = -mlog- * log- + log — 1 = — + o (l). (15) np nq a \ a /
Кроме того, из (15) log P {q = m} = — (яр + га) log (1 + — — («I ~ log (1 + log —1 == r- + O (1) = n доказывает асимптотику (13). Людмила Фирмаль
Смотрите также:
Предмет теория вероятностей и математическая статистика
| Биномиальное распределение | Интегральная предельная теорема Муавра-Лапласа |
| Теорема Пуассона | Применения предельных теорем |

