Оглавление:
Логарифмы
а) Логарифм числа b, где b > 0, по основанию а, где а > 0, 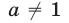 (обозначается
(обозначается 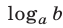 ), — показатель степени, в которую нужно возвести число а, чтобы получить число b , т. е.
), — показатель степени, в которую нужно возвести число а, чтобы получить число b , т. е.
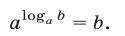
Это равенство называют основным логарифмическим тождеством.
Логарифм числа а по основанию 10 называют десятичным и обозначают 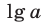 , а логарифм числа а по основанию е называют натуральным и обозначают
, а логарифм числа а по основанию е называют натуральным и обозначают 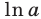 .
.
б) Свойства логарифмов.
Если 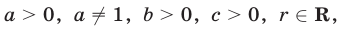 то
то
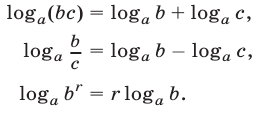
В частности,
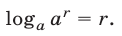
в) Формула перехода к новому основанию.
Если 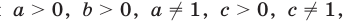 то
то 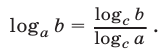
Эта формула называется формулой перехода от логарифма по основанию а к логарифму по основанию с. Частные случаи формулы перехода:
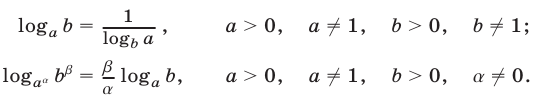
Пример №19.
Освободиться от иррациональности в знаменателе дроби
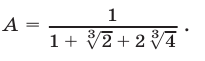
Решение:
Обозначим 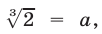 тогда
тогда 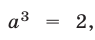
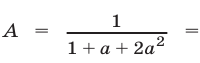
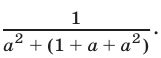 Умножая числитель и знаменатель полученной дроби на
Умножая числитель и знаменатель полученной дроби на  и применяя формулу разности кубов, запишем А в следующем виде:
и применяя формулу разности кубов, запишем А в следующем виде:
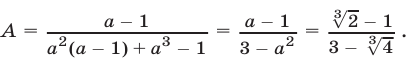
Снова применяя формулу разности кубов, получаем
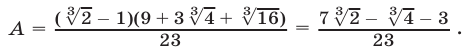
Ответ: 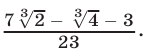
Пример №20.
Доказать, что
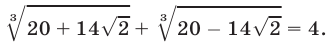
Доказательство. Пусть 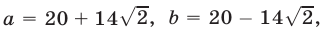
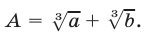 Применяя формулу куба суммы и учитывая, что
Применяя формулу куба суммы и учитывая, что 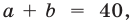
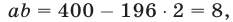 получаем
получаем
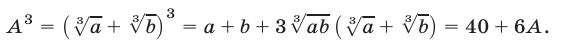
Таким образом, левая часть А рассматриваемого равенства является корнем уравнения
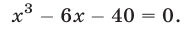
Это уравнение имеет корень 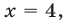 а его левую часть можно записать в виде
а его левую часть можно записать в виде 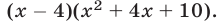 Так как уравнение
Так как уравнение 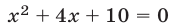 не имеет действительных корней, а левая часть равенства А — действительное число, то
не имеет действительных корней, а левая часть равенства А — действительное число, то
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

