Оглавление:
Логарифмическое дифференцирование
В ряде случаев для нахождения производной целесообразно заданную функцию сначала, прологарифмировать. А затем результат продифференцировать. Такую операцию называют логарифмическим дифференцированием.
Пример №22.1.
Найти производную функции
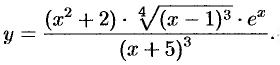
Решение:
Можно найти 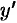 с помощью правил и формул дифференцирования. Однако такой способ слишком громоздкий. Применим логарифмическое дифференцирование. Логарифмируем функцию:
с помощью правил и формул дифференцирования. Однако такой способ слишком громоздкий. Применим логарифмическое дифференцирование. Логарифмируем функцию:
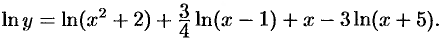
Дифференцируем это равенство по  :
:
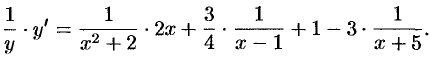
Выражаем 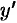 :
:
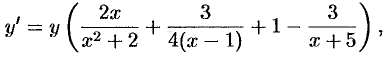
т.е.
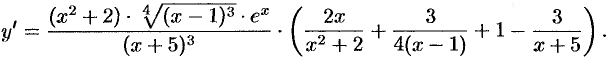
Существуют функции, производные которых находят лишь логарифмическим дифференцированием. К их числу относится так называемая степенно-показательная функция 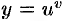 , где
, где 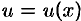 и
и 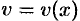 — заданные дифференцируемые функции от
— заданные дифференцируемые функции от  . Найдем производную этой функции:
. Найдем производную этой функции:
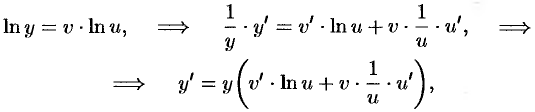
т.е.
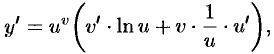
или
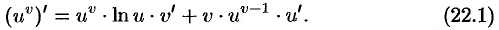
Сформулируем правило запоминания формулы (22.1): производная степенно-показательной функции равна сумме производной показательной функции, при условии 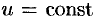 , и производной степенной функции, при условии.
, и производной степенной функции, при условии.
Дополнительный пример №22.2.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Дифференцирование неявно заданной функции |
| Дифференцирование функции, заданной параметрически |
| Производные высших порядков явно заданной функции |
| Механический смысл производной второго порядка |

