Оглавление:
Логарифмические уравнения
Справочные сведения
1.Логарифмическая функция 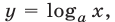 где
где 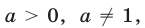 определена при
определена при 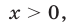 множество ее значений есть
множество ее значений есть 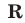 .
.
2.Показательная и логарифмическая функция являются взаимно обратными. Это означает, что
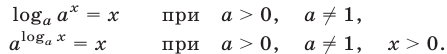
3.Основные свойства логарифмов выражают следующие формулы, справедливые при 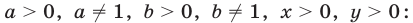
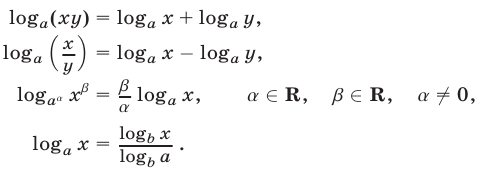
Замечание, а) Левые и правые части первых двух равенств определены на разных множествах: в правых частях этих равенств 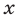 и
и 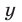 могут принимать только положительные значения, а левые части определены при любых значениях
могут принимать только положительные значения, а левые части определены при любых значениях 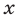 и
и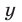 одного знака, т. е. при
одного знака, т. е. при 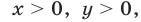 а также при
а также при 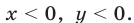
б) При решении логарифмических уравнений часто используется формула
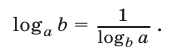
4.При решении логарифмических уравнений применяют следующие преобразования:
а) замену функции 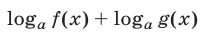 на функцию
на функцию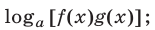
б) замену функции 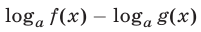 на функцию
на функцию 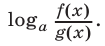
Эти преобразования, основанные на свойствах логарифмов, являются допустимыми.
Обратные замены могут привести к потере корней исходного уравнения из-за возможного сужения ОДЗ уравнения. Чтобы избежать потери корней, следует заменять функции 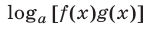
и 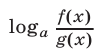 на функции
на функции 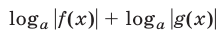 и
и 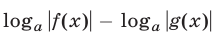 соответственно. Такие преобразования являются допустимыми. Приведем еще формулу
соответственно. Такие преобразования являются допустимыми. Приведем еще формулу
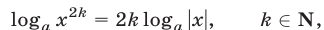
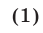
применяемую при решении логарифмических уравнений, и обратим внимание на то, что отбрасывание знака модуля в правой части равенства (1) — грубая ошибка, которую, к сожалению, часто допускают абитуриенты.
5. Сформулируем утверждения, относящиеся к решению логарифмических уравнений.
а) Простейшее логарифмическое уравнение
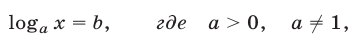
имеет единственный корень 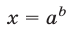 при любом
при любом 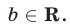
б) Потенцирование, т. е. переход от уравнения

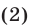
к уравнению
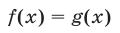
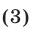
является допустимым преобразованием, а уравнение (3) — следствием уравнения (2).
Обратный переход (логарифмирование), т. е. переход от уравнения (3) к уравнению (2), может привести к потере корней.
Уравнения (2) и (3) равносильны, если хотя бы одна из функций 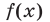 ,
, 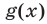 принимает только положительные значения.
принимает только положительные значения.
Примеры с решениями
Пример №94.
Решить уравнение 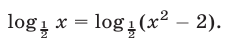
Решение:
Потенцируя, получаем уравнение 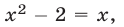 являющееся следствием исходного и имеющее корни
являющееся следствием исходного и имеющее корни 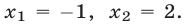 Проверка показывает, что
Проверка показывает, что 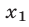 не удовлетворяет уравнению (
не удовлетворяет уравнению ( 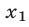 не входит в ОДЗ уравнения), а число
не входит в ОДЗ уравнения), а число 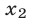 — корень исходного уравнения.
— корень исходного уравнения.
Ответ. 
Пример №95.
Решить уравнение
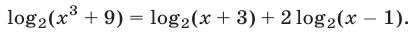
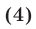
Решение:
Заменив в правой части уравнения (4) сумму логарифмов на логарифм произведения, получим уравнение
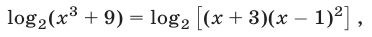
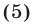
которое является следствием уравнения (4). При этом преобразовании посторонние корни могут появиться благодаря расширению ОДЗ уравнения.
Потенцируя, получаем уравнение
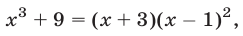
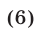
являющееся следствием уравнений (4) и (5). Уравнение (6) можно заменить равносильным уравнением 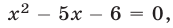 которое имеет корни
которое имеет корни 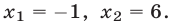
Число —1 не содержится в ОДЗ уравнения (4), а число 6 входит в ОДЗ этого уравнения и является его корнем.
Ответ.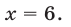
Пример №96.
Решить уравнение
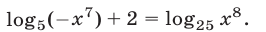
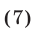
Решение:
Заметим, что ОДЗ уравнения (7) — множество отрицательных чисел. Пусть 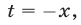 тогда
тогда 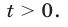 Используя формулу
Используя формулу
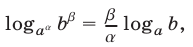
запишем уравнение (7) в виде
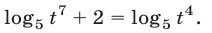
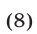
Так как 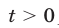 , то уравнение (8) равносильно уравнению
, то уравнение (8) равносильно уравнению
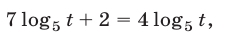
откуда находим 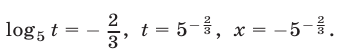
Ответ. 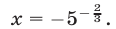
Пример №97.
Решить уравнение
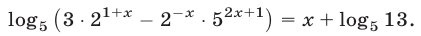
Решение:
Так как правую часть уравнения (9) можно записать в виде 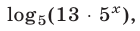 где
где 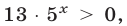 то потенцирование приводит к уравнению
то потенцирование приводит к уравнению
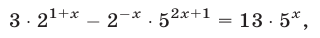
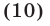
равносильному уравнению (9).
Разделив обе части уравнения (10) на 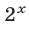 и обозначив
и обозначив 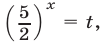 получим уравнение
получим уравнение 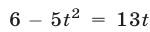 или
или 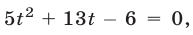 имеющее корни
имеющее корни 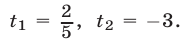 Следовательно, уравнение (10) равносильно совокупности уравнений
Следовательно, уравнение (10) равносильно совокупности уравнений 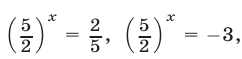 , откуда следует, что
, откуда следует, что 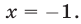
Ответ. 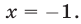
Пример №98.
Решить уравнение
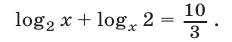
Решение:
Пусть 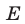 — множество чисел
— множество чисел 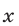 таких, что
таких, что

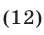
Тогда 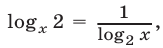 и уравнение (11) примет вид
и уравнение (11) примет вид 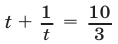 или
или 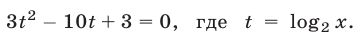 Отсюда находим
Отсюда находим 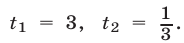 Если
Если 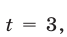 то
то 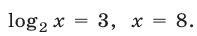 Если
Если 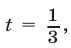 то
то 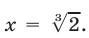 Найденные значения
Найденные значения 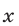 удовлетворяют условиям (12) и являются корнями уравнения (11).
удовлетворяют условиям (12) и являются корнями уравнения (11).
Ответ. 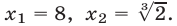
Эта ссылка возможно вам будет полезна:
Пример №99.
Решить уравнение
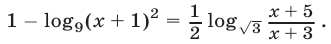
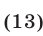
Решение:
Переходя к логарифмам по основанию 3, получаем уравнение
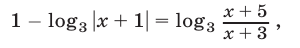
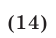 равносильное уравнению (13).
равносильное уравнению (13).
Уравнение
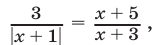
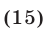
полученное из уравнения (14) в результате потенцирования, является следствием уравнения (14).
При решении уравнения (15) нужно рассмотреть два возможных случая: 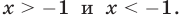
Если 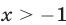 , то
, то 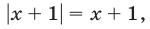 и уравнение (15) примет вид
и уравнение (15) примет вид
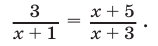
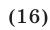
Умножая обе части уравнения (16) на 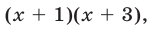 получим уравнение
получим уравнение 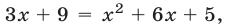 являющееся следствием уравнения (16) и имеющее корни
являющееся следствием уравнения (16) и имеющее корни 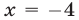 (не удовлетворяет условию
(не удовлетворяет условию  и
и 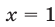 .
.
Аналогично, если 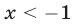 , то уравнение (15) преобразуется к виду
, то уравнение (15) преобразуется к виду 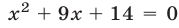 , откуда находим
, откуда находим 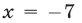 и
и 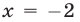 (оба корня меньше, чем
(оба корня меньше, чем 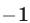 ). Проверка показывает, что числа
). Проверка показывает, что числа 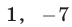 и
и 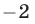 входят в ОДЗ уравнения (13) и являются его корнями.
входят в ОДЗ уравнения (13) и являются его корнями.
Ответ.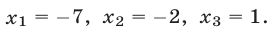
Замечание. Многие абитуриенты при решении уравнения (13) допустили ошибку, отбросив знак модуля в левой части уравнения (14). Это привело к потере корней 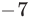 и
и 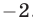 .
.
Пример №100.
Решить уравнение
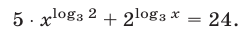
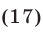
Решение:
Заметим, что
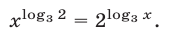
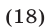
Равенство (18) является верным при всех х > 0, так как логарифмы по основанию 3 его левой и правой частей совпадают. Используя равенство (18), заменим уравнение (17) равносильным уравнением 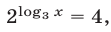 откуда
откуда 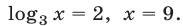
Ответ. 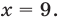
Пример №101.
Решить уравнение
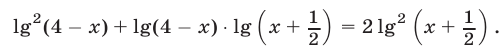
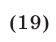
Решение:
Используя тождество 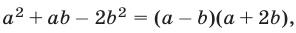 заменим уравнение (19) следующим равносильным уравнением:
заменим уравнение (19) следующим равносильным уравнением:
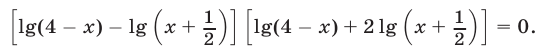
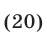 Уравнение (20) равносильно совокупности уравнений:
Уравнение (20) равносильно совокупности уравнений:
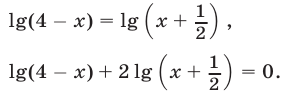
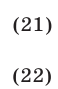
Потенцируя, из (21) и (22) получаем уравнения
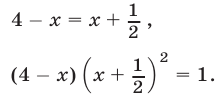
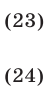
Уравнение (23) имеет корень 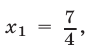 а уравнение (24) приводится к виду
а уравнение (24) приводится к виду 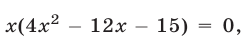 откуда
откуда 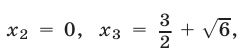
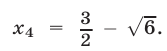 Корнями исходного уравнения (19) являются те и только те из чисел
Корнями исходного уравнения (19) являются те и только те из чисел 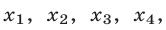 которые входят в ОДЗ уравнения (19), т. е. удовлетворяют условию
которые входят в ОДЗ уравнения (19), т. е. удовлетворяют условию 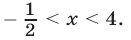
Ответ. 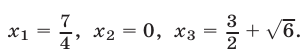
При решении уравнений, содержащих функции вида 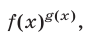 следует иметь в виду, что:
следует иметь в виду, что:
а) если 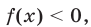 то выражение
то выражение 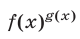 не имеет смысла;
не имеет смысла;
б) если 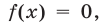 то это выражение считается равным нулю при
то это выражение считается равным нулю при 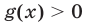 и не имеющим смысла при
и не имеющим смысла при 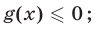
в) при 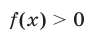 функция
функция 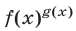 определяется формулой
определяется формулой
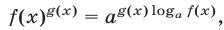
где 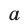 — любое положительное число, не равное единице;
— любое положительное число, не равное единице;
г) функция вида 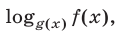 где
где 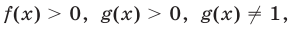 определяется формулой
определяется формулой
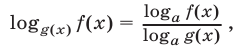
где 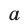 — любое положительное число, не равное единице.
— любое положительное число, не равное единице.
Пример №102.
Решить уравнение
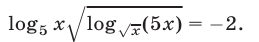
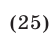
Решение:
Данное уравнение имеет смысл, если 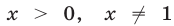 и
и 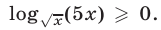 Переходя к логарифмам по основанию 5 и возведя обе его части в квадрат, получаем уравнение
Переходя к логарифмам по основанию 5 и возведя обе его части в квадрат, получаем уравнение
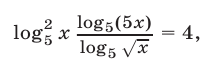
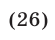
являющееся следствием уравнения (25).
Уравнение (26) можно записать в виде 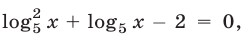 откуда
откуда 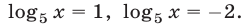
Значение 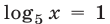 следует отбросить, так как в этом случае левая часть равенства (25) неотрицательна. Итак,
следует отбросить, так как в этом случае левая часть равенства (25) неотрицательна. Итак, 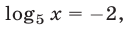 откуда
откуда 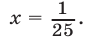 Проверка показывает, что число
Проверка показывает, что число 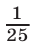 — корень уравнения (25).
— корень уравнения (25).
Ответ. 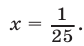
Пример №103.
Решить уравнение
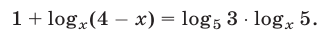
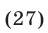
Решение:
Так как 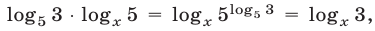 то уравнение (27) можно записать в виде
то уравнение (27) можно записать в виде 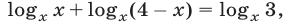 откуда получаем уравнение
откуда получаем уравнение
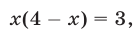
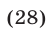
являющееся следствием уравнения (27). Из уравнения (28) находим 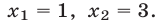 При
При 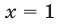 уравнение (27) теряет смысл, а число
уравнение (27) теряет смысл, а число 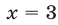 — корень уравнения (27).
— корень уравнения (27).
Ответ.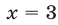
Пример №104.
Решить уравнение
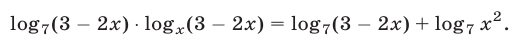
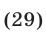
Решение:
Допустимые значения 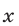 определяются условиями
определяются условиями
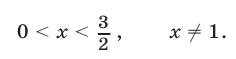
Переходя к логарифмам по основанию 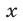 , запишем уравнение (29) в виде
, запишем уравнение (29) в виде
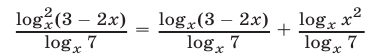
или
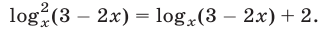
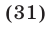
Из уравнения (31), являющегося следствием уравнения (29), находим 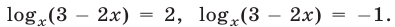 Если
Если 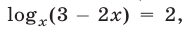 то
то 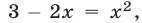 откуда
откуда 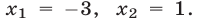 Если
Если 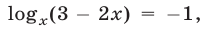 то
то 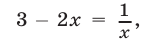 откуда
откуда 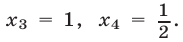
Условиям (30) удовлетворяет
только число 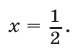
Ответ. 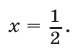
Пример №105.
Решить уравнение
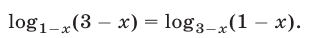
Решение:
Область допустимых значений уравнения (32) — множество 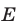 точек
точек 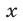 таких, что
таких, что 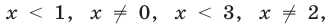 откуда находим
откуда находим
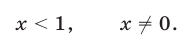
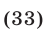
Применяя формулу 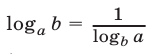 и полагая
и полагая 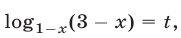 получаем уравнение
получаем уравнение 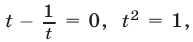 откуда
откуда 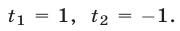 Следовательно, на множестве
Следовательно, на множестве 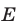 уравнение (32) равносильно совокупности уравнений
уравнение (32) равносильно совокупности уравнений 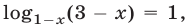
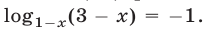 Первое из них не имеет корней, так как
Первое из них не имеет корней, так как 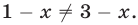 Второе уравнение равносильно на множестве
Второе уравнение равносильно на множестве 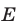 уравнению
уравнению 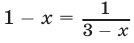 или
или 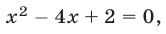 откуда
откуда 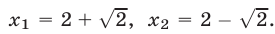 Из чисел
Из чисел 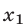 ,
, 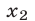 только
только 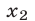 удовлетворяет условиям (33) и является корнем уравнения (32).
удовлетворяет условиям (33) и является корнем уравнения (32).
Ответ.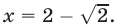
Пример №106.
Решить уравнение 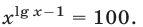
Решение:
Логарифмируя обе части уравнения по основанию 10, получим равносильное уравнение 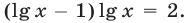 Полагая
Полагая 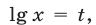 запишем это уравнение в виде
запишем это уравнение в виде 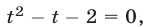 откуда
откуда 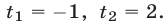 Решив уравнения
Решив уравнения 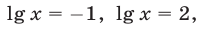 найдем
найдем 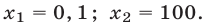
Ответ. 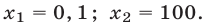
Пример №106.
Решить уравнение
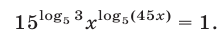
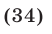
Решение:
Уравнение (34) равносильно каждому из следующих уравнений:
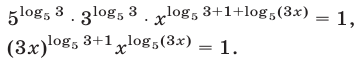
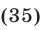
Логарифмируя уравнение (35) по основанию 5, получаем
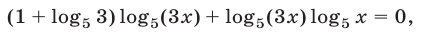
или

Если 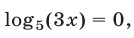 то
то 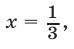 а если
а если 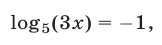 то
то 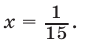
Ответ. 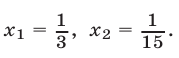
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

