Решение логарифмических неравенств основано на том, что функция 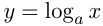 при
при 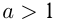 является монотонно возрастающей, а при
является монотонно возрастающей, а при 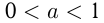 — монотонно убывающей. Отсюда следует:
— монотонно убывающей. Отсюда следует:
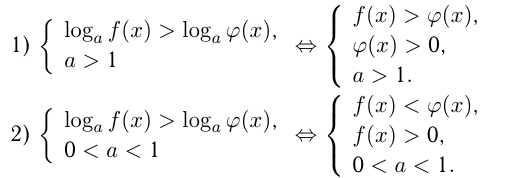
При избавлении от знака логарифма, т.е. при потенцировании, очень важно не забывать об ограничениях на аргумент и основание логарифма. Простейшие логарифмические неравенства:
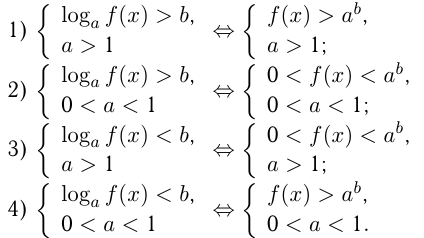
Все преобразования в логарифмических неравенствах аналогичны преобразованиям в логарифмических уравнениях. Важную роль играют переход к новому основанию логарифма, упрощение логарифмического выражения, разложение на множители.
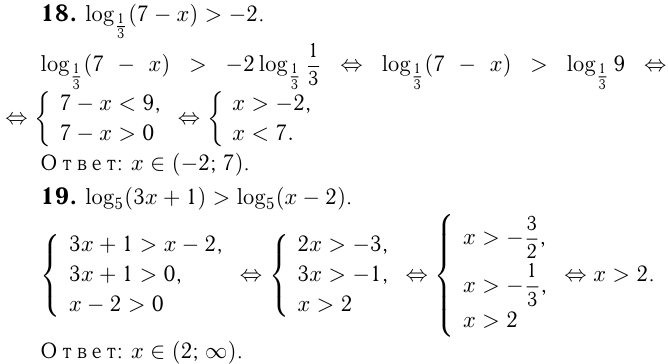


Только крайний левый интервал удовлетворяет всем трем неравенствам.
О т в е т: 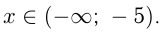
Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Неравенства с радикалами задачи с решением |
| Показательные неравенства задачи с решением |
| Тригонометрические неравенства задачи с решением |
| Решение рациональных неравенств |
