Оглавление:

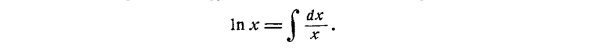

Логарифмическая, показательная и тригонометрические функции действительного переменного
- Логарифмическая функция, индикаторная функция, тригонометрическая функция действительных переменных Количество существенно различных типов функций, с которыми мы сталкивались в предыдущей главе, невелико. Наиболее важными из них являются полиномы, дробные рациональные функции, алгебраические функции, явные и неявные и тригонометрические функции, прямые и обратные функции.
Как правило, эти новые функции были введены, потому что было невозможно решить некоторые проблемы, которые привлекали внимание математиков с помощью ранее известных функций. Этот процесс можно сравнить с введением иррациональных и комплексных чисел, которые были впервые введены в связи с тем, что некоторые алгебраические уравнения не могут быть решены с использованием класса известных чисел.
Постепенное расширение математических знаний сопровождалось введением для анализа функциональных классов один за другим Людмила Фирмаль
Одним из богатейших источников новых функций были интеграционные задачи. Была сделана попытка интегрировать несколько функций f (x) по известным функциям. Эти попытки потерпели неудачу, и после серии неудачных попыток родилась идея, что эта задача была принципиально неразрешимой. Иногда можно было доказать, что это действительно так, но в принципе строгие доказательства таких фактов были обнаружены гораздо позже. В целом математики быстро осознали невозможность представления определенных интегралов с известными функциями, убедившись, что попытки найти такие представления не увенчались успехом.
Затем была введена новая функция F (x), которая определяется свойством F (x) = f (x). Основываясь на этом определении, свойства F (x) t были исследованы, и было обнаружено, что F (x) обладает свойствами, которые не может иметь конечная комбинация известных функций. Поэтому обоснованность исходного предположения о невозможности необходимого представления этой функции была установлена. Один из таких случаев произошел, когда вы были в главе на этой странице книги. Определить функцию VI l: используя уравнение 1 c dx ln * = J- •
| Однозначность степенного ряда | Определение In x |
| Умножение рядов | Характер стремления In x: к бесконечности при возрастании х |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Давайте рассмотрим, в чем причина веры. Действительно новая функция. Мы уже видели, что эта функция не может быть рационально-дробной, потому что рационально-рациональная производная всегда является десятичной рациональной функцией, знаменатель которой содержит только несколько факторов (например, XLH.4). Вопрос о том, не может ли эта функция быть алгебраической или тригонометрической, является более сложным. Однако многие попытки легко убедить, что дифференциация никогда не сможет освободить вас от алгебраической иррациональности.
Например, результат дифференцирования всегда в -fl — \ — x раз превосходит произведение -fx с рациональной рациональной функцией, и такая же ситуация имеет место во всех случаях. Дифференцирование функции, содержащей sin l: или cos *, всегда приводит к одной из этих функций. Таким образом, хотя нет строгих доказательств того, что 1пх является новой функцией (и не претендует на 1), есть разумные основания для подтверждения этого.
Поэтому, когда вы так точно думаете, вы можете увидеть, что свойства сильно отличаются от свойств тех функций, с которыми вы встречались до сих пор. Людмила Фирмаль

