Оглавление:


Логарифмическая функция
- Логарифмическая функция. Логарифмическая функция определяется как обратная экспоненциальной функции. Пусть[с, (!]- Это любой
отрезок бесконечной линии. В этом сегменте, функции y=Ах, а>1 возрастает и непрерывными. Так, благодаря теореме 4.5,
функция y=1(x)=Ah находится в отрезке [AC, AA], а непрерывная обратная Людмила Фирмаль
функция x=C'(y), которая называется~'(Y)=^E AU-аргумент y, заменяющий аргумент y на x и заменяющий обозначение функции x
на y, записывается в более употребительном виде.: _ г / =1оэа%. * Требования co)=1 могут оказаться результатом остальных требований (и поэтому могут быть опущены).146Ч. 4. Непрерывность функций
- Случай 00, В>\и все полу-постоянного тока х>0 в<0 < а<1,и 11t1o§х= — ОО,Pt1o§х=+ОО при > 1, х — >0~}»0х->•]1ОО подача it-1§м х=4-У,11§х= — ОО at0<а < 1. X-xn-0 * достоверность этих свойств следует за свойствами
экспоненциальной функции. 3)любое положительное Ху и Х^1о^а (Х]•Х2)=1о§а1 4-1о^Х2. Это свойство также следует экспоненциальному свойству. З а м е ч а н и Е. следует подчеркнуть логарифм функции y=1o^e x, где e=11T1 4—.
Для этой функции используется имя g/=1ph. Людмила Фирмаль
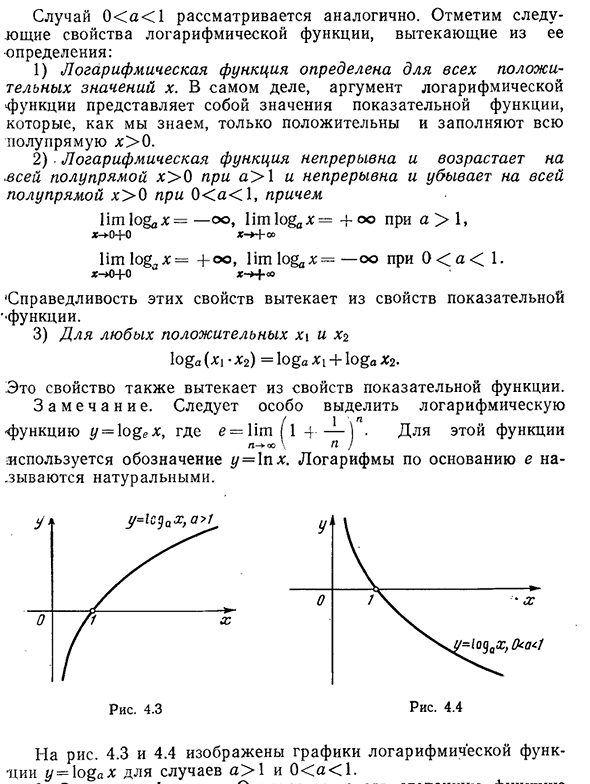
Логарифм, основанный на E, называется естественным. Для риса. 4. 3 и 4. 4-графики логарифмической функции y — \o§A x, где случай a>1 и 0<a<1
Смотрите также:
Методическое пособие по математическому анализу
| Отсутствие разрывов первого рода и устранимых разрывов у производной. | Степенная функция |
| Производная векторной функции | Общая схема отыскания экстремумов |

