Пример решения задачи №19.
Лодка переплывает реку, выдерживая направление перпендикулярно берегу. Скорость лодки относительно берега v = 1 м/с, скорость течения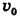 
= 0,8 м/с. Чему равен вектор скорости лодки 
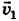относительно воды? За какое минимальное время 
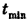лодка переплывет эту реку с прежней по модулю скоростью относительно воды, если ширина реки Н = 100 м? Какова при этом будет скорость лодки относительно берега 
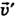? За какое время t лодка переплывет реку, пройдя минимальный путь?
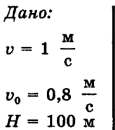
Решение:
Свяжем неподвижную систему отсчета с берегом, а движущуюся — с течением. Тогда скорость течения 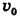— это переносная скорость, а скорость лодки относительно течения 
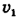— собственная скорость и, наконец, скорость лодки относительно берега v — абсолютная скорость.
Отметим, что все эти названия условны, ведь мы можем связать неподвижную систему отсчета с самим течением реки, и тогда двигаться будет берег, и именно с ним надо будет связать движущуюся систему отсчета, и при этом названия скоростей изменятся.
Ведь все инерциальные системы отсчета согласно принципу относительности Галилея равноправны. Просто нам привычнее связывать неподвижную систему отсчета с берегом (с пристанью, с деревом на берегу и т. п.), потому что на берегу мы находимся все же чаще, чем в лодке.
Но если связать неподвижную систему отсчета с движущимся телом (с течением, с вагоном, с самолетом и т. п.),то иногда решение задачи оказывается проще. И еще, необязательно пользоваться только «нашими» индексами при обозначении скоростей, вы можете выбрать любые индексы, например, 
. и т. п. Но всегда надо помнить: разные скорости (или иные величины) надо обозначать разными индексами, и это обозначение надо сохранять на протяжении всего решения. Иными словами, нельзя разные величины обозначать одной и той же буквой с одним и тем же индексом и нельзя обозначение одной и той же величины (букву или индекс) изменять в процессе решения.
Чтобы определить вектор собственной скорости лодки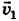, т. е. ее скорости относительно воды, надо определить его модуль 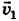и угол 
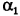между вектором 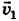и, например, берегом (а можно между вектором 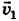и направлением течения реки или между 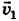и перпендикуляром к течению, и т. п.). Обратимся к рис. 4-8, а). Согласно правилу сложения скоростей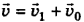 
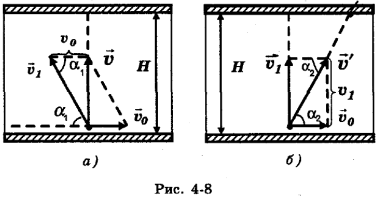
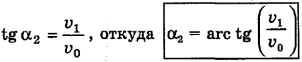
Но при решении задач мы пользуемся скалярными величинами. Чтобы определить модуль вектора искомой скорости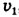 
, можно воспользоваться теоремой Пифагора, ведь в треугольнике скоростей на рис. 4-8, а) вектор 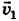является гипотенузой, а векторы 
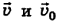— катетами, поэтому 
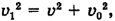, откуда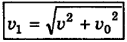 
Направление вектора 
, т. е. угол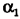 
между вектором и берегом, определим из того же треугольника скоростей, ведь этот угол и угол 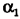в треугольнике скоростей равны, как накрест лежащие углы при параллельных и секущей. Из треугольника скоростей
Напомним, что выдерживая направление движения перпендикулярно берегу, лодка пройдет минимальный путь, равный ширине реки Н. Определим, за сколько времени t она пройдет этот путь. Поскольку движение лодки равномерное, для определения времени t достаточно разделить ширину реки Н на скорость р, с которой лодка пройдет минимальный путь Н, двигаясь перпендикулярно течению: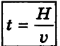 
Теперь определим, за какое минимальное время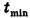 
лодка может переплыть эту реку, двигаясь со скоростью 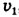. Время движения лодки 
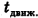через реку зависит не только от скорости лодки и ширины реки, но и от угла а между направлением течения и лодки. В методических указаниях к решению задач приведена формула, показывающая, как зависит время переплывания реки от этого угла а при неизменных Н и 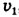Запишем ее еще раз:
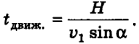
Очевидно, что чтобы частное 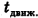от деления Н на 
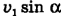было минимальным при неизменных Н и 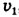, надо, чтобы 
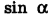был максимальным. Но максимальное значение синуса угла равно единице, и такому 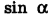соответствует угол 
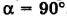. Следовательно,
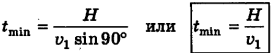
Для определения скорости лодки относительно берега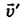 
(здесь « штрих» при букве 
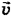— просто индекс, а не знак производной) обратимся к рис. 4-8, б). Из этого рисунка следует, что скорость лодки 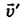является гипотенузой в треугольнике скоростей 
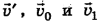, а переносная скорость 
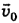и собственная скорость 
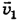— катетами. По теореме Пифагора модуль вектора
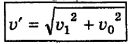
И наконец, угол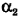 
между вектором 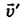и берегом (или между и’ и течением реки, т. е. вектором 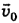) определим из треугольника скоростей:
Задача в общем виде решена. Подставим в формулы (1)-(6) численные значения величин, известные из условия задачи, и выполним вычисления:
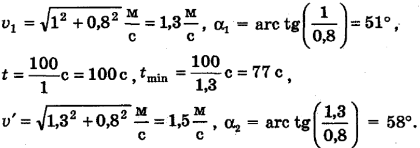
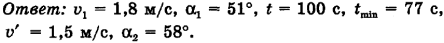
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:
