Оглавление:

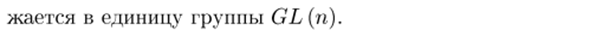

Линейные представления групп. Терминология
- Линейное представление группы. Срок действия. Определение Линейное представление конечной группы G Пространственное евклидово пространство En является картой / Это помещает каждый элемент в этой группе Поскольку соответствие является линейным преобразованием.
- Ta пространства En, Для любых a1 и a2 в G выполняется соотношение T (aiCL2) = TaiTa2. Пространственное евклидово пространство En является гомоморфизмом этой группы Py для подмножества этого линейного преобразования Пространство. Используются следующие термины: Пространство En называется Пространство выражения, размерность n этого пространства.
Следовательно, конечное линейное представление группы G. Людмила Фирмаль
Пространство называется измерением выражения. Здесь Ep называется основой выражения. Гомоморфный образ f (G) группы G имеет вид Выражение этой группы в пространстве выражений. Ниже, для краткости, n-мерное линейное представление Группа называется простым представлением этой группы.
Используйте символы для обозначения представления группы G бык D (G); Dex (например, D ^) (G)). D ^) (г) Линейное преобразование, соответствующее элементу (линейный оператор) G∈G в выражении D ^) (G) Тривиальное представление группы G называется гомоморфизмом Отображение G (n) в элементы идентичности GL.
- Отображение группы G в подгруппу GL (n) изо- В случае морфизма выражение называется точным. Очевидно, что не все группы имеют точные n-мерные представления Например, для группы O A0) это не может Точное одномерное представление (в частности, Группа O A) является абелевой, а группа O A0) не является абелевой.
Гомоморфизм / под группой G GL (n) Полученное групповое представление изоморфно фактору В группе G / kern /, где kern / — так называемое ядро гомоморфизма /.
То есть набор G элементов, которые отображаются в группу GL (n) тождеств при гомоморфизме /. Людмила Фирмаль
Смотрите также:
| Группа Лоренца | Матрицы линейных представлений. Эквивалентные представления |
| Унитарные группы | Приводимые и неприводимые представления |

