Оглавление:



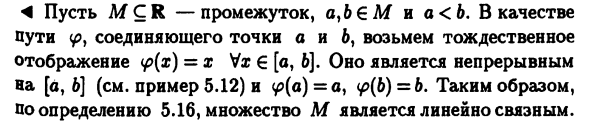

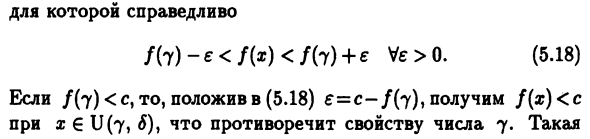




Линейно связные множества
- Интуиция имеет несколько подмножеств Метрическое пространство можно рассматривать как единое целое (Например, интервалы и сегменты на числовой линии R, кружки Плоскость R2, Rn шарики), другие подмножества Может состоять из нескольких отдельных «частей» (например, Объединение двух интервалов или сегментов R без В общем, объединение двух окружностей в R2 Есть что-то общее: оно дополняет некоторые круги в R2. Далее меня интересует набор, представляющий: Нечто целое. Чтобы прояснить эту интуитивную концепцию Введите следующее определение: Определение 5.16.
Отображение некоторых отрезков числовой линии R [a, / 3] (a) = a и (p (p) = b В этом случае они называются путями (или дугами), соединяющими точки 6. В этом случае сами точки а и 6 называются Начало и конец пути соответственно. Следовательно, линейно связное пространство является метрикой Пространство, где могут существовать любые две точки Связано каким-то образом. Pass изображение y? ([A, p]) содержит эту точку, 6 / 3]). Путь <р пересекает подмножество LSM . Очевидно, две точки a и 6 множества M Будет каким-то образом подключен 0 \ (6) = 6, но если М = LieВ, Кроме того, если LPS = 0, выбрав \ € A и b \ £ B,
Метрическое пространство М Какой бы ни была точка, это называется линейной связью И в этом пространстве б имеет такую непрерывность Людмила Фирмаль
Такой сегмент [c * i, /? я] может быть выбран. Это будет функция у? (X) = x отображается последовательно в M (функция M а f (a) -e 0 (когда € = c-a> 0) Неравенство f (x) c для x ^ x * (В этом случае достаточно положить ξ = b-o 0). Следовательно, в этом случае это φsup A. Следовательно, 7 / (г)> с. / Непрерывно в разделе [а, (3}) в разделе 7 Есть S районов Это справедливо fh) -e <Нет. 0. (5,18) Если f (j) <c1, установка (5.18) = = c- / (7) дает f (x) <c a: € U (7, #), это противоречит седьмому свойству
Ситуация также возникает, когда f (7)> c. так / (7) = s► Доказательство теоремы 5.11. Заявление. Предложение 5.3. Вери действительная функция f (x) Вещественная переменная x € R непрерывна на отрезке [a, p] и f (a) = a, f (p) = 6 и a <c <6, тогда Такая точка 7 «<7 </? А / (7) = с. Это утверждение сыграет важную роль в будущем. Часто упоминается как промежуточная теорема. Фактическое значение непрерывной функции. особенно Если f (oi) f (P) <0, то есть функции на обоих концах сегмента Ненулевое значение с другим знаком, следующий — правда Заявление. Заявление 5.4. Вери действительная функция f (x) Непрерывный в сегменте [a, / 3], в конце сегмента
- Различное значение знака, точки в сегменте 7, где / (7) = 0. Свойства отображения набора линейных соединений Установите следующую теорему. Теорема 5.12. Линейно связанное метрическое изображение Пространство для непрерывного отображения является линейным Связанное метрическое пространство. <f: X- * Y — непрерывное отображение Метрическое пространство X, линейно связанное с метрикой U пространство. Докажем, что изображение f (X) является линейным Связанное метрическое пространство. Рассмотрим любые две точки / (а) и / (/?) Установите f (X). Поскольку X связан линейно, точка а и /? Согласно определению 5.16 Т.е. есть непрерывная карта <p <P (a) = o множеству [A, f] C R некоторого отрезка = 6.
Тогда карта / о (р Построение непрерывного отображения (см. Теорему 5.8). Это Сегмент карты [a, (3}) для установки f (X) / Io)) = / (a) и / (* («) = / (*). ► Мы можем сделать этот вывод из теоремы 5.11 и 5.12. Следствие 5.5. Актуальная функция непрерывной дизентерии Set A «линейно подключен, его значение установлено Пролет числовой линии. <На самом деле, линейное соединение является непрерывным Множество X (x) множества f (X) CR функции f имеет вид Согласно теореме 5.12, линейно связаны, Применить теорему 5.11. ► Это свойство реальных функций часто формулируется Непрерывно как промежуточное свойство Набор линейно связанных функций: любые две Значение такой функции принимает все промежуточные значения Значение между ними.
Смотрите также:
| Определение непрерывного отображения | Равномерная непрерывность |
| Свойства непрерывного отображения множеств | Переменные величины |

