Линейная статистическая модель

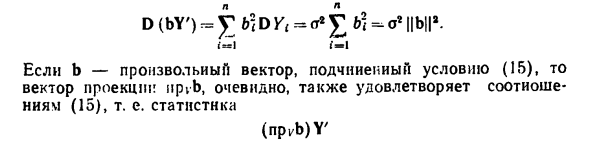
Линейная статистическая модель

• Определим линейную статистическую модель, полагая, что векторные наблюдатели? = (У’Ь У2, …, У „) имеет следующую струк- структуру: Y ^ XQ ‘+ ae’, или? = ВГ + ае, A0) где Х = [хц, 1 = 1, …. п; / = 1, …, г], г ^ п, -известная числовая матрица, 8 = (8ь …, 9г) -вектор неизвестных коэффициентов, е = (еь ег ея) -случайный вектор, такой, что Ме, = 0, i = l п, [Ме.-е /, «, / = 1, …. п] = /, A1) «> 0— неизвестный параметр, / -единичная матрица. Из A0) получить, что вектор математических ожиданий наб- наблюдательный равенство а матрица ковариаций Ry = [cov (Kj, К /), i, / = 1 n] = /? 0е = a2 / /.

Введем видим так что Х = [х, ‘, х2’, …, х /], и A0) можно записать в виде Y = 8iX | + 82X2 + … + 8rXr + a.A2) Свое название модель A2) получила за то, что неизвестный век- вектор среднего 8 … + 8гхг лежит в линейном подпространстве VczRn, порожденном пространстве- модели А2, модель А2) можно задать в непараметризованном виде: A3) где V-заданное каким-либо способом линейное подпространство- подпространство, порождающих V, приходим к форме А2). в форме A2) порождающих векторов. 4.

Несмещенные оценки с минимальной дисперсией: матрица полного ранга. Людмила Фирмаль

Пусть -Несмещенная оценка для где а = (а, аг) -пронзвольный числовой вектор. что математическое ожидание оценки м (bY ‘) =? & <мк <= b (elX; -г … + efX;) = охьх; + … + егьх; тождественно по 8 |, …, Qr встречает с ав «, откуда получают Ьх, ‘= аи …. bx / = 5r, илн ЪХ = а. A5) Условие A5) является необходимым и достаточным, чтобы статистика bY ‘несмещенно оценивала аЭ’.

Дисперсия оценки D (bY ‘) = jr b] D Yt = a * Если б-указанный вектор, подчиненный условию А5), то вектор проекции npvb, очевидно, также удовлетворяет соотноше- соотношениям A5), т. е. статистика (np.b) Y ‘ 74 несмещенно оценивает значение аЭ ‘, и в то же время ее дисперсия с учетом теоремы Пифагора удовлетворяет неравенству D ((npvb) Y ‘) = a2 || npvb |! 2 <a2 || b || 2 = D (bY’).

• Отсюда следует, что в поисках линейной несмещенной оценки с минимальной дисперсией можно ограничиться лежащими в подпространстве V: Ь = С | Х, + … + с, хг = сХ ‘. A6) Подставляя A6) в A5), приходим к системе уравнений для оп- определение с (ср. (8), (9)): сХ’А ^ а. A7) Допустим, матрица X имеет полный ранг г.

-‘, и наилучшая линейная несмещенная оценка A ‘/ y. A8) Выбирая a = 6, = F, i, б, 2 6, я) .где 6 </ = 0 при 1ф) и 6, <= 1 (символ Кронекера), получим иесмещенную линейную оценку для О, с минимальной дисперсией: % = bi (X’X) — ^ X ‘\’. A9) Организуя оценки Qt в вектор-версии 6 = (8 |, …. 8г) и замечая, что [б /, …. бл ‘] = /, запишем вектор наилучших линейных несме- несмещенных оценок: Q ‘= (X’X) -XX’ \ ‘. B0)

Тогда матрица Х’Х невырождена, A7) имеет единственное решение при любом век- векторе а: с = а (Х’Л ‘) Людмила Фирмаль

Наилучшая несмещенная оценка A8) параметрической функции Таким образом, доказано Георема Г. (Гаусс, Марков). Если матрица X линейной мо- модели имеют полный ранг, то лучшие линейные несмещенные оценки параметров 8, -даются формулой B0) .Если а = (аь … ¦ .., а,) — линейный несмещенный вектор несмещенная оценка параметрической функции дисперсия единственна и дается формулой аб ‘.

Смотрите также:

Предмет статистики

Сравнение дисперсии в двух выборках	Наилучшие оценки в случае матрицы неполного ранга
Примеры линейных моделей	Наилучшие оценки как оценки наименьших квадратов