Оглавление:
Уравнение 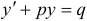 , где
, где 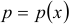 и
и 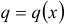 — заданные непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
— заданные непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Если функция 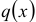 , стоящая в правой части уравнения, тождественно равна нулю, т.е.
, стоящая в правой части уравнения, тождественно равна нулю, т.е. 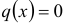 , то уравнение называется линейным однородным, в противном случае — линейным неоднородным.
, то уравнение называется линейным однородным, в противном случае — линейным неоднородным.
Таким образом, 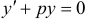 — линейное однородное уравнение, а
— линейное однородное уравнение, а 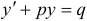 — линейное неоднородное уравнение.
— линейное неоднородное уравнение.
Рассмотрим два метода интегрирования линейных уравнений
1 метод.
Для решения уравнения применяют подстановку 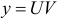 , причем функцию
, причем функцию 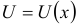 считают новой неизвестной функцией, а функцию
считают новой неизвестной функцией, а функцию 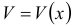 подчиняют условию:
подчиняют условию: 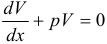 . Данная подстановка приводит к двум уравнениям с разделяющимися переменными относительно
. Данная подстановка приводит к двум уравнениям с разделяющимися переменными относительно 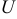 и
и 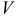 . Произведение полученных функций даст общее решение линейного уравнения:
. Произведение полученных функций даст общее решение линейного уравнения: 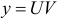 .
.
Пример 1.
Решить уравнение 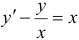 .
.
Решение:
Здесь 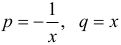 . Имеем:
. Имеем: 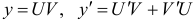 .
.
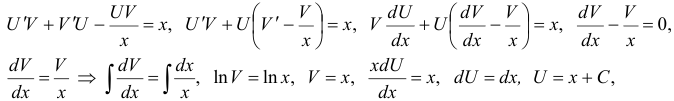
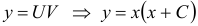 — общее решение линейного уравнения.
— общее решение линейного уравнения.
2 метод (Метод вариации произвольной постоянной).
В линейном однородном уравнении 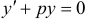 переменные разделяются и его общее решение, которое мы обозначим через
переменные разделяются и его общее решение, которое мы обозначим через 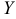 , легко находится. Затем находят общее решение неоднородного линейного уравнения
, легко находится. Затем находят общее решение неоднородного линейного уравнения 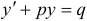 , считая, что оно имеет такую же форму, как и общее решение соответствующего однородного уравнения
, считая, что оно имеет такую же форму, как и общее решение соответствующего однородного уравнения 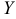 , но где
, но где 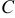 есть не постоянная величина, а неизвестная функция от
есть не постоянная величина, а неизвестная функция от 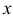 , т.е. считая, что
, т.е. считая, что 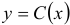 .
.
Полученное общее решение состоит из двух слагаемых: общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.
Пример 2.
Найти общее решение уравнения 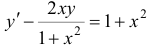 .
.
Решение:
Интегрируем соответствующее однородное уравнение:
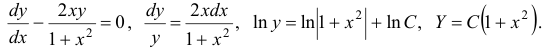
Считаем 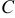 функцией
функцией 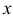 :
: 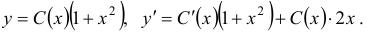
Подставляем в исходное уравнение:
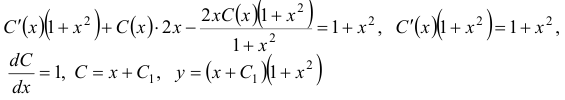
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Уравнения с разделяющимися переменными |
| Однородные уравнения первого порядка |
| Уравнение Бернулли |
| Уравнения вида y(n) = f(x) |

