Оглавление:
Линейные уравнения. Уравнение Я. Бернулли
Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде
где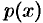 
и 
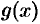— заданные функции, в частности — постоянные.
Особенность ДУ (48.11): искомая функция 
и ее производная входят в уравнение в первой степени, не перемножаясь между собой.
Рассмотрим два метода интегрирования ДУ (48.11) — метод И. Бернулли и метод Лагранжа.
Метод И. Бернулли
Решение уравнения (48.11) ищется в виде произведения двух других функций, т. е. с помощью подстановки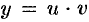 
, где 
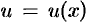и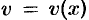 
— неизвестные функции от 
, причем одна из них произвольна (но не равна нулю — действительно любую функцию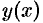 
можно записать как
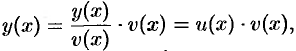
где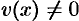 
). Тогда 
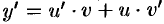. Подставляя выражения и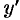 
в уравнение (48.11), получаем: 
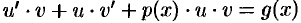или
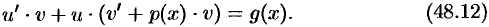
Подберем функцию 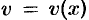так, чтобы выражение в скобках было равно нулю, т. е. решим 
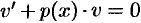. Итак, 
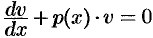, т. е. 
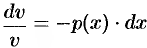. Интегрируя, получаем:
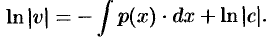
Ввиду свободы выбора функции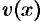 
, можно принять 
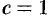. Отсюда
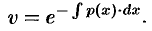
Подставляя найденную функцию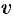 
в уравнение (48.12), получаем
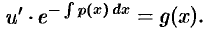
Получено уравнение с разделяющимися переменными. Решаем его:
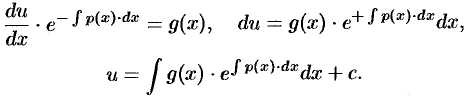
Возвращаясь к переменной , получаем решение
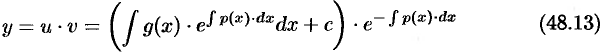
исходного ДУ (48.11).
Пример №48.8.
Проинтегрировать уравнение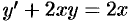 
.
Решение:
Полагаем 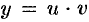. Тогда 
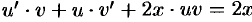, т. е. 
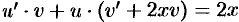. Сначала решаем уравнение 
:
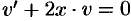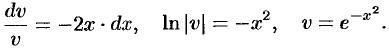
Теперь решаем уравнение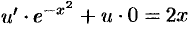 
, т. е.
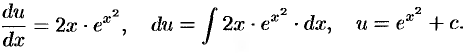
Итак, общее решение данного уравнения есть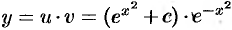 
, т. е. 
.
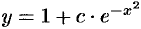На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Уравнения с разделяющимися переменными |
| Однородные дифференциальные уравнения |
| Метод вариации произвольных постоянных |
| Уравнение в полных дифференциалах интегрирующий множитель |
