Оглавление:
Линейные однородные ДУ n-го порядка
Полученные результаты можно распространить на линейные однородные дифференциальные уравнения n-го порядка, имеющие вид
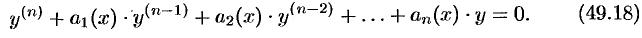
1. Если функции 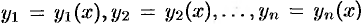 являются частными решениями уравнения (49.18), то его решением является и функция
являются частными решениями уравнения (49.18), то его решением является и функция 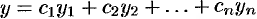 .
.
2.Функции 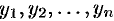 называются линейно независимыми на
называются линейно независимыми на  , если равенство
, если равенство  выполняется лишь в случае, когда все числа
выполняется лишь в случае, когда все числа 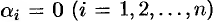 ; в противном случае (если хотя бы одно из чисел
; в противном случае (если хотя бы одно из чисел 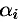 , не равно нулю) функции
, не равно нулю) функции 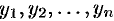 — линейно зависимы.
— линейно зависимы.
3. Определитель Вронского имеет вид
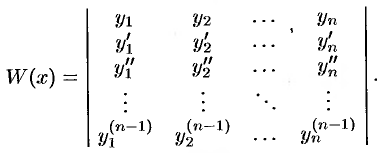
4. Частные решения 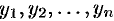 уравнения (49.18) образуют фундаментальную систему решений на
уравнения (49.18) образуют фундаментальную систему решений на  , если ни в одной тючке этого интервала вронскиан не обращается в нуль, т. е.
, если ни в одной тючке этого интервала вронскиан не обращается в нуль, т. е. 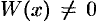 для всех
для всех 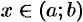 .
.
5. Общею решение ЛОДУ (49.18) имеет вид 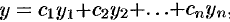 , где
, где 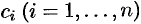 — произвольные постоянные,
— произвольные постоянные, 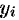 — частные решения уравнения (49.18), образующие фундаментальную систему.
— частные решения уравнения (49.18), образующие фундаментальную систему.
Пример №49.6.
Показать, что функции 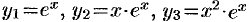 образуют фундаментальную систему решений некоторого ЛОДУ третьего порядка (дополнительно: составить это уравнение).
образуют фундаментальную систему решений некоторого ЛОДУ третьего порядка (дополнительно: составить это уравнение).
Решение:
Найдем 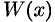 :
:
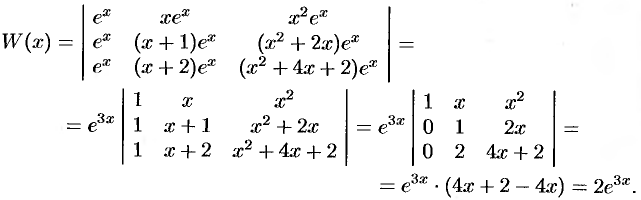
Ясно, что 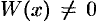 для всех
для всех 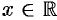 . Следовательно, данные функции образуют фундаментальную систему решений ЛОДУ третьего порядка. В общем виде ЛОДУ третьего порядка выглядит так:
. Следовательно, данные функции образуют фундаментальную систему решений ЛОДУ третьего порядка. В общем виде ЛОДУ третьего порядка выглядит так:
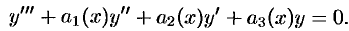
Подставив функции 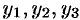 в это уравнение, получим систему из грех уравнений относительно функций
в это уравнение, получим систему из грех уравнений относительно функций 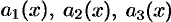 . Решая ее, получим ЛОДУ
. Решая ее, получим ЛОДУ 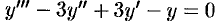 ; его общее решение:
; его общее решение:
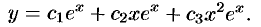
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:

