Оглавление:
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида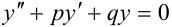 
, где 
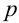и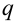 
— постоянные величины.
Например, уравнения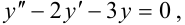 
, 
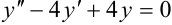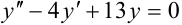являются линейными однородными дифференциальными уравнениями второго порядка с постоянными коэффициентами
Для нахождения решения дифференциальных уравнений такого вида будем составлять характеристическое уравнени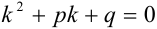е 
, где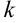 
— некоторая новая переменная. Характеристическое уравнение является квадратным относительно .
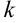В зависимости от числа и вида корней данного характеристического уравнения, решение исходного дифференциального уравнения можно представить в виде таблицы 4.1:
Таблица 41.1
Решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
Рассмотрим решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами на конкретных примерах.
Пример №41.3.
Решите дифференциальное уравнение: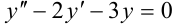 
.
Решение:
Составим характеристическое уравнение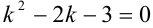 
. Найдем его корни. 
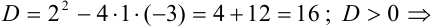существуют два различных корня 
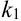и 
.
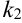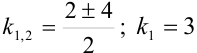или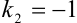 
.
Тогда, пользуясь таблицей 41.1, находим общее решение дифференциального уравнения по формуле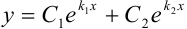 
: 
.
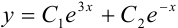Ответ: .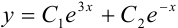
Пример №41.4.
Решите дифференциальное уравнение: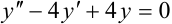 
.
Решение:
Составим характеристическое уравнение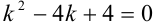 
. Найдем его корни. 
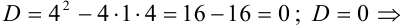существуют два равных корня 
.
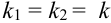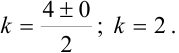
Тогда, пользуясь таблицей 41.1, находим общее решение дифференциального уравнения по формуле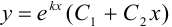 
: 
.
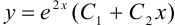Ответ: .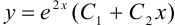
Пример №41.5.
Решите дифференциальное уравнение: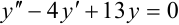 
.
Решение:
Составим характеристическое уравнение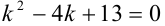 
. Найдем его корни. 
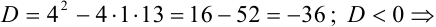существуют два комплексных корня 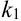и .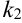
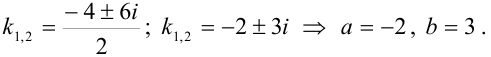
Тогда, пользуясь таблицей 41.1, находим общее решение дифференциального уравнения по формуле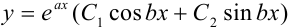 
: 
.
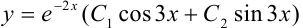Ответ: .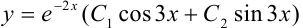
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Методика решения линейных дифференциальных уравнений первого порядка. |
| Простейшие дифференциального уравнения второго порядка. |
| Понятие мнимой единицы. |
| Алгебраическая форма комплексного числа. |
