Оглавление:
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Дифференциальное уравнение вида
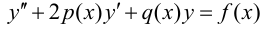
называется линейным неоднородным дифференциальным уравнением. При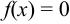 
уравнение называется линейным однородным.
Общее решение линейного однородного ДУ имеет вид
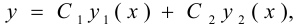
где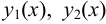 
— два линейно независимых частных решения.
Для неоднородного линейного уравнения общее решение имеет вид:
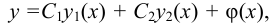
где 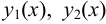— частные решения линейного однородного уравнения, соответствующего неоднородному, а 
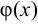— частное решение неоднородного уравнения.
Линейное дифференциальное уравнение
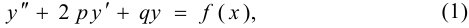
где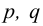 
— постоянные величины, называется линейным дифференциальным уравнением с постоянными коэффициентами.
Решение этого уравнения ищется в виде
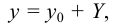
где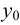 
— общее решение соответствующего однородного уравнения
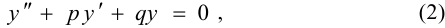
a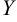 
— частное решение неоднородного уравнения (1).
Для нахождения общего решения уравнения (2) составляют характеристическое уравнение
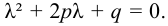
Для этого уравнения возможны три случая.
1. 
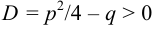, корни уравнения 
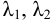вещественные и 
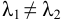, то общее решение уравнения (2) имеет вид:
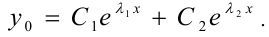
2. 
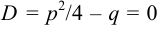, корни уравнения 
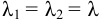— вещественные, то общее решение уравнения (2) имеет вид:
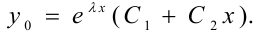
3. 
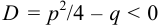. Обозначим 
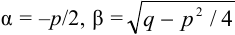, тогда общее решение уравнения (2) будет иметь вид:
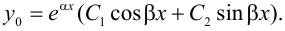
Частное решение 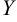уравнения (1) может быть найдено методом неопределённых коэффициентов в следующих простейших случаях:
1. 
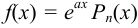, где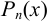 
— многочлен степени 
.
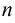Если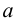 
не является корнем характеристического уравнения, то частное решение ищем в виде:
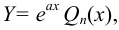
где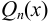 
— многочлен степени 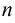с неопределёнными коэффициентами.
Если 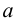является корнем характеристического уравнения, то полагают
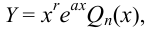
где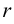 
— кратность корня .
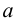2. 
.
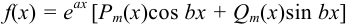Если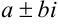 
не являются корнями характеристического уравнения, то полагают
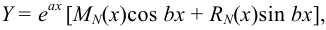
где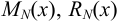 
— многочлены степени 
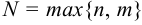с неопределёнными коэффициентами.
Если 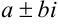— корни характеристического уравнения, то
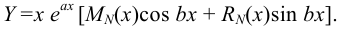
Задача №102.
Решить ДУ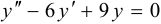 
.
Решение:
Составим характеристическое уравнение
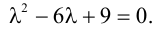
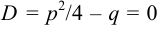, т. e. 
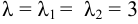, тогда
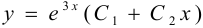— общее решение ДУ.
Задача №103.
Найти общее решение уравнения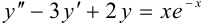 
.
Составим характеристическое уравнение
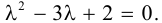
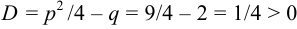, т. е. 
.
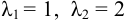Общее решение соответствующего однородного уравнения
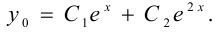
Правая часть данного уравнения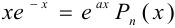 
, причём 
, 
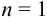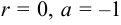. Поэтому частное решение исходного уравнения ищем в виде:
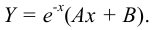
Найдём первую и вторую производную:
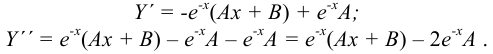
Подставляем данные выражения в исходное уравнение:
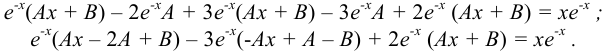
Сократим на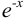 
и приравняем друг другу коэффициенты при 
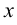и свободные члены левой и правой частей равенства. Находим:
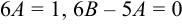, откуда 
.
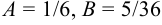Следовательно,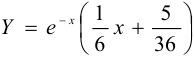 
, а общее решение заданного уравнения имеет вид 
.
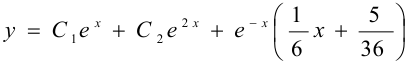Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
