Оглавление:
Линейные дифференциальные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка называется уравнение вида
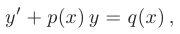
где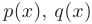 
— заданные непрерывные функции аргумента 
.
Решение линейного уравнения ищут в виде
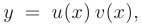
где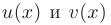 
— новые неизвестные функции. Подставляя в исходное уравнение
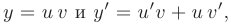
будем иметь:
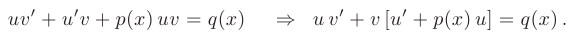
Подберем функцию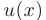 
так, чтобы выражение, содержащееся в квадратной скобке, обращалось в нуль:
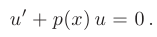
В результате исходное уравнение преобразуется к виду
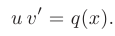
Оба уравнения являются уравнениями с разделяющимися переменными. Решая первое уравнение находим функцию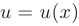 
.
Выполняем подстановку найденной функции во второе уравнение, которое после этого принимает вид
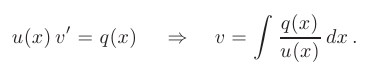
Интегрирование последнего выражения позволяет определить вторую неизвестную функцию
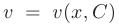
и, перемножив функции, записать общее решение линейного дифференциального уравнения первого порядка
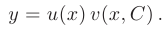
Теорема 7.1. (Существования и единственности решения дифференциальных уравнений первого порядка.) Если в дифференциальном уравнении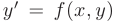 
функция 
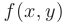и её частная производная 
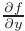непрерывны на открытом множестве 
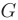координатной плоскости 
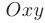, то для всякой точки 
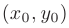множества 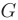найдется единственное решение 
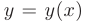данного уравнения, удовлетворяющее условию 
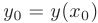. Т.е. через каждую точку 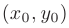множества 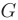в оговоренных условиях проходит одна и только одна интегральная кривая данного уравнения.
Пример:
Найти частное решение линейного дифференциального уравнения первого порядка, удовлетворяющее начальному условию:
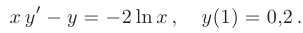
► Разделим обе части уравнения наги представим искомую функцию в виде произведения двух новых неизвестных функций:
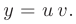
В таком случае исходное дифференциальное уравнение может быть записано в виде
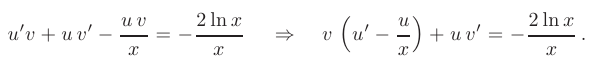
Выберем функцию 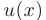так, чтобы выражение в скобках равнялось нулю. В результате, от линейного дифференциального уравнения перейдем к системе из двух дифференциальных уравнений, причем в первом из них переменные 
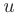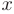и разделяются:
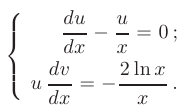
Из первого уравнения системы находим функцию 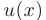: d
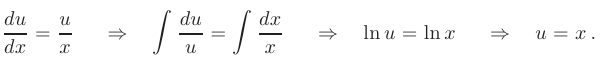
Заметим, что при интегрировании последнего выражения произвольную постоянную можно положить равной нулю, так как для решения всей системы достаточно найти частное решение первого уравнения.
Подставим полученное решение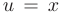 
во второе уравнение системы. В результате тоже получим дифференциальное уравнение первого порядка с разделяющимися переменными:
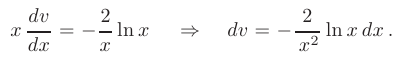
Функцию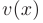 
найдем в результате интегрирования по частям:
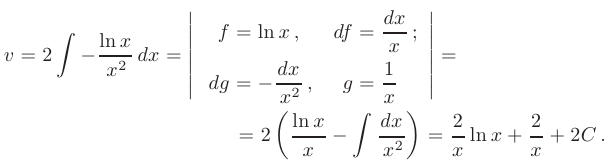
Таким образом, общее решение линейного дифференциального уравнения первого порядка имеет вид:
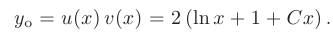
Частное решение получим из общего, используя для определения произвольной постоянной заданное начальное условие:
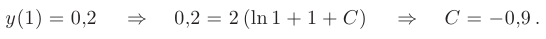
После подстановки найденного значения постоянной интегрирования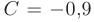 
в общее решение, искомое частное решение линейного дифференциального уравнения принимает вид
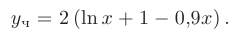
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
