Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами в математике

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

Рассмотрим метод решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами:

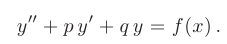
Теорема 7.4. Общее решение линейного неоднородного дифференциального уравнения 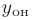представляет собой сумму общего решения соответствующего однородного уравнения 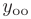и какого-либо частного решения исходного неоднородного уравнения :

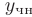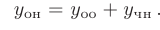
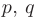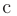Таким образом, чтобы найти общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами и правой частью специального вида 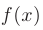необходимы следующие действия:

1. Отбросив правую часть, найти общее решение однородного дифференциального уравнения (см. предыдущий раздел).
2. Указать вид частного решения неоднородного дифференциального уравнения в соответствии с правой частью .
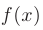3. Найти числовые значения неопределенных коэффициентов и записать частное решение дифференциального уравнения 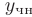(см. в этом разделе далее).
4. Записать общее решение неоднородного дифференциального уравнения 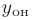в виде суммы найденных выше общего 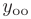и частного решения .

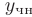Вид частного решения неоднородного дифференциального уравнения 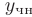зависит от вида функции 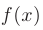, стоящей в его правой части. Рассмотрим два наиболее простых случая.

1 случай. Пусть правая часть имеет вид

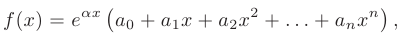
где 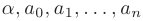— заданные постоянные коэффициенты. Тогда частное решение неоднородного дифференциального уравнения 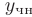имеет вид

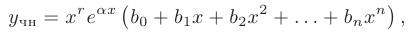
где 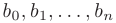— неопределенные коэффициенты.

Константа 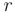равна числу совпадений параметра а с корнями характеристического уравнения:

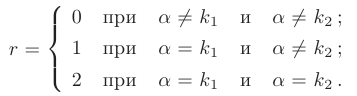
Значения неопределенных коэффициентов 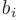определяют, исходя из того, что 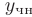является решением исходного дифференциального уравнения. Для этого следует продифференцировать функцию 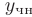два раза (учитывая, что коэффициенты 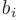являются константами), подставить выражения для 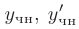и 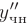в исходное дифференциальное уравнение. После сокращения на общий множитель 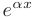и приведения подобных, нужно сгруппировать слагаемые по степеням переменной 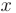. Приравнивая коэффициенты при одинаковых степенях 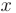в левой и правой частях полученного уравнения, переходят к системе уравнений относительно неизвестных коэффициентов 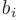. Решив эту систему, записывают частное решение 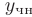с найденными значениями коэффициентов .

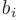Пример:

Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами

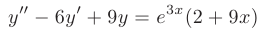
► Составим характеристическое уравнение:

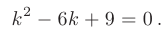
Дискриминант уравнения равен нулю:

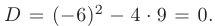
В таком случае, корни характеристического уравнения действительные, кратные:

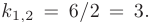
Следовательно, общее решение однородного дифференциального уравнения, соответствующего исходному, имеет вид

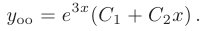
Выпишем правую часть данного дифференциального уравнения:

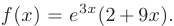
Так как в правой части присутствует множитель 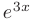, то 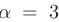. Также заметим, что число 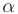совпадает с кратными корнями характеристического уравнения: 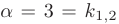. Отсюда следует, что 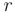= 2.

Наличие множителя 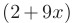в правой части неоднородного дифференциального уравнения говорит о том, что частное решение будет содержать многочлен первого порядка с двумя неизвестными коэффициентами:

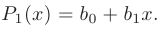
В результате, частное решение неоднородного дифференциального уравнения будет иметь вид

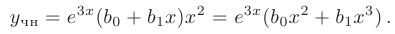
Для определения неизвестных коэффициентов 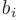дважды продифференцируем полученную форму частного решения:

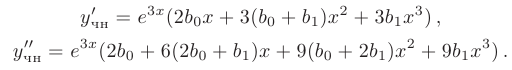
Подставим выражения для 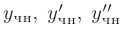в исходное дифференциальное уравнение. После сокращения на общий множитель 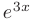, приведения подобных и группировки по степеням переменной 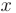получим следующее уравнение:

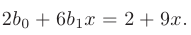
Приравнивая коэффициенты при одинаковых степенях переменной 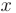, перейдем к эквивалентной системе уравнений:

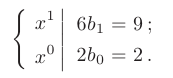
Отсюда находим значения неизвестных коэффициентов:

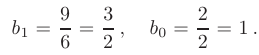
В итоге, частное решение неоднородного дифференциального уравнения записывается в виде

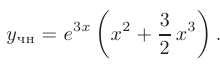
Тогда, искомое общее решение примет вид

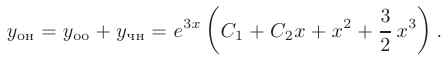
2 случай. Пусть правая часть линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

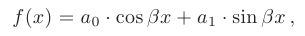
где 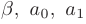— некоторые действительные числа, причем 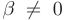. В этом случае частное решение неоднородного дифференциального уравнения 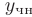примет вид

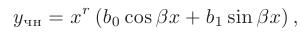
где 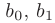— неизвестные коэффициенты. Константа 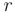равна либо 0 либо 1:

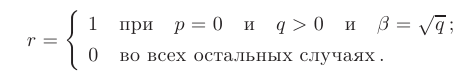
Отыскать значения неопределенных коэффициентов 6; следует так же, как и в случае I с одной разницей: после приведения подобных, группировку слагаемых производят при одинаковых функциях переменной 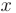, т. е. приравнивают коэффициенты при функциях

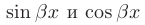
в левой и правой частях полученного уравнения.