Оглавление:
Задача №1.1.11.
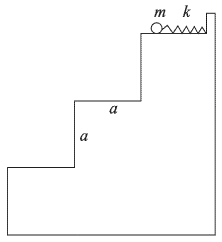
Лестница состоит из трех одинаковых гладких ступенек ширины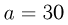 
и такой же высоты. На верхней ступеньке расположена в плоскости рисунка невесомая пружина жесткостью 
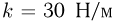, правым концом прикрепленная к неподвижной стенке, а левым — упирающаяся в лежащий на ступеньке маленький шарик массой 
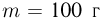. Шарик сдвигают вправо, сжимая пружину, после чего отпускают без начальной скорости. До какой максимальной величины 
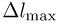можно сжать пружину, чтобы выпущенный шарик по одному разу коснулся средней и нижней ступенек? Удар шарика о ступеньку считать абсолютно упругим, трение и сопротивление воздуха не учитывать. Ускорение свободного падения принять 
.
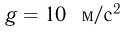Решение:
Сжатая пружина сообщает шарику начальную скорость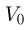 
, величина которой может быть найдена из закона сохранения энергии: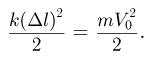
Отсюда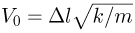 
, т.е. начальная скорость шарика пропорциональна сжатию пружины. Покинув с такой скоростью верхнюю ступеньку. шарик летит по параболической траектории до соударения с другими ступеньками. При упругом ударе о каждую из них горизонтальная составляющая скорости шарика не изменяется, а вертикальная составляющая скорости шарика меняет направление на противоположное, сохраняя свою величину. В результате угол между нормалью к ступеньке и скоростью шарика перед соударением оказывается равным по величине углу между нормалью к ступеньке и скоростью шарика после соударения; модуль скорости шарика после соударений не изменяется. По условию задачи максимальная начальная скорость шарика отвечает случаю, когда шарик отскакивает от средней ступеньки и попадает на самый край нижней ступеньки. Соответствующая траектория шарика изображена на рисунке штриховой линией. Заметим, что если начальная скорость шарика превысит данное значение, он пролетит над нижней ступенькой, не коснувшись ее. Дальнейшее увеличение начальной скорости шарика может привести к тому, что он не попадет и на среднюю ступеньку.
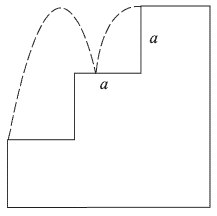
Время падения шарика, не имеющего вертикальной скорости, с высоты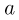 
равно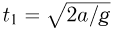 
. Такое же время шарик будет подниматься до уровня верхней ступеньки после соударения со средней ступенькой. Наконец, падать с высоты верхней ступеньки до удара о нижнюю ступеньку шарик будет в течение времени 
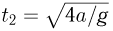. Таким образом, полное время движения шарика с момента, когда он покидает верхнюю ступеньку, до соударения с нижней ступенькой равно:
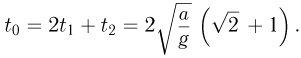
За это время шарик смещается по горизонтали на расстояние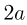 
. Следовательно,
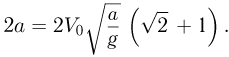
Объединяя последнее равенство с выписанным соотношением между начальной скоростью шарика и сжатием пружины, получаем ответ: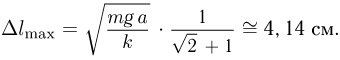
Эти задачи взяты со страницы решения задач по физической механике:
Решение задач по физической механике
Возможно эти задачи вам будут полезны:
