Оглавление:
Лемма о распределении гидродинамического давления в плавноизменяющемся движении
Лемма о распределении гидродинамического давления в плавноизменяющемся движении. Как упоминалось в 4.3, плавное изменяющееся движение имеет небольшую кривизну обтекаемой линии и очень малый угол расхождения между обтекаемой линией. Уравнения движения Эйлера для невязких жидкостей могут быть выражены в виде (4.15). Колено следовательно, в случае основного потока вязкой жидкости в установившемся движении(рис. 4.13).
При этом движении кривизна элементарных струек, из которых состоит поток жидкости, весьма незначительна и очень мал также угол расхождения между осями отдельных струек поэтому поперечные сечения потока можно рассматривать как плоские сечения, нормальные к оси потока. Людмила Фирмаль
- Чтобы получить левое-правое единообразие неравенства (4.59), необходимо добавить дополнительный член/ g * ’к right. It показывает расход определенной энергии на преодоление сопротивления при перемещении реальной (вязкой)жидкости между первой и второй секциями. D в данном случае. Уравнение Бернулли принимает следующий вид: Ров. И затем <И’ <1 сиг ’ рассмотрим плавное изменение движения с почти линейными линиями тока, которые почти параллельны оси x (рис.4.14).
Поскольку нет движения вдоль оси y и оси z, есть только 1 компонент их скоростей, а еще 1 yy да 0 и yy да 0 и соответствующие Ускорение да 0 и да Да 0.Если подставить эти значения в уравнения Эйлера (4.15), то получим: 1 др р ДХ 1 др Р-до.〜 ■ ^+2 р ДГ 1 + икс= + Год= окей. РГ. Снова. 1. 2-й. = Р2 + ^ + 2 ^ Пе И 9 −2 ^ + Ч * Т (4.60） Часть энергии, затраченной на преодоление гидравлического сопротивления, преобразуется из механической в тепловую, и этот процесс необратим.
- Это называется Энергия dissipation. In в связи с этим, вы можете рассмотреть ку? Энергия пропала. D. течения вязкой жидкости при выводе уравнения Бернулли, прежде всего, необходимо учитывать распределение давления плавно меняющегося движения и 2 леммы из 3 интегралов. 1 врач Г _ ди ДХ ш р л(ц> ■ 4 + Y = 0; Строка 1 1 др р ДГ + 2 = 0. (4.61） Первое уравнение системы(4.61) это уравнения движения, остальные 2-дифференциальные уравнения равновесия жидкости относительно оси NR.
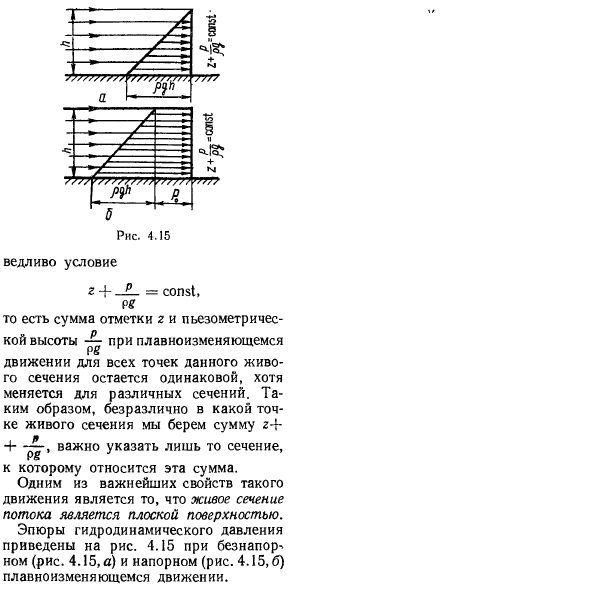
В плоскости yOG, перпендикулярной направлению движения, гидродинамическое давление распределяется по закону гидростатического pressure. As вы можете видеть, что плоскость yOg совпадает с живым поперечным сечением flow. In связь с этим、 64. Как дела? р + -, у, = const1 Снова. То есть сумма метки r и плавно меняющейся пьезометрической высоты.
В заключение отметим, что дифференциальные уравнения движения были получены для идеальной (невязкой) жидкости, которая отличается от реальной отсутствием сил трения. Людмила Фирмаль
- Движение всех точек определенного живого участка остается одинаковым, но для каждого оно разное section. So, в какой момент в живом разделе r + 4-d, важно указать только этот раздел、 Связано с этой суммой. 1. одной из важнейших характеристик такого движения является то, что живое сечение потока представляет собой плоскую поверхность. На рисунке показано гидродинамическое давление. 4.15, без давления (рис.4.15, а) и плавное изменяющееся движение при давлении (рис. 4.15.6).
Смотрите также:
Возможно эти страницы вам будут полезны:
- Примеры плоских потенциальных движений жидкости.
- Уравнение Д. Бернулли для элементарной струйки установившегося движения жидкости.
- Лемма о трех интегралах (по Н. Н. Павловскому).
- Уравнение Д. Бернулли для потока жидкости
