Оглавление:




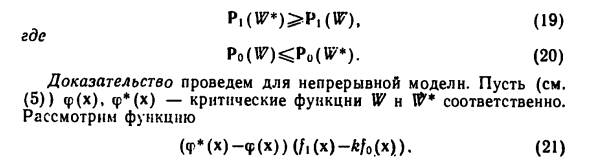



Лемма Неймана—Пирсона
- Рассмотрим статистическую модель вида C0 ‘, &, (Po, PJ). Здесь, Семейство вероятностных измерений состоит только из двух компонентов. Предполагается, что Яо: P = Po, I,: P = P1, (8) То есть для каждой из гипотез Ho и H \ распределение выборки Полностью определен. Такая гипотеза называется простой (и В приведенных выше примерах (I) и (II) нулевая гипотеза Просто, альтернатива не простая). Критерии Максимальная мощность в случае (8) присутствует всегда. потому что Степенная функция критерия Wa в утверждении (8) имеет вид Есть две вероятности: Далее, задача поиска лучшей критической области будет
Следующим образом: все подмножества № „? # Равенство .’9) Все ва ^ A0) Объясните, как организован этот набор, а затем нарисуйте Формальные доказательства. Сначала рассмотрим следующую простую вещь Ситуация: #? = (), X2 Xn), Po ( <) = LM, * = 1, …, N 216 Во-первых, условие (9) выполняется только для prn a = a * = k = 1, 2, …. N — 1. равенство Содержит подмножество ваков, которые правильно составлены От к делу. с того времени
Понятно, что вы заказали вероятность И положить Wak = {iXfi ik). A1) Прибытие в собственность A0). Людмила Фирмаль
Рассмотрим другой частный случай: набор SB такой же, Но Po (* <) = m, где δ> 0, предположим, что m является целым числом Числовое значение, то есть набор вероятностей Po (* i), * = 1. •••• N — это Соответствующие номера. Преобразуйте эту модель и замените каждую элемент x> 8B на m, элемент x (A), … xi (mi) и положить = 1 миля i ~ l H), Po (, (/)) — = b, -Pi () / «/./= 1 миля. I = l .-. ‘V. Очевидно, исходная статистическая модель взята из трансформатора. Преобразование путем добавления и объединения групп элементов Соответствующая вероятность.
Оптимальный набор новых моделей A модели получается так же, как A1), упорядочивая пары (/, /). лунный промежуток средней полной воды который Пирог ( Поскольку вероятности Ti (* <(/)) равны друг другу, И может выполнить любой фиксированный я, порядок А2) Соблюдайте следующие свойства: вероятность Pi (*, • (/)),. / = 1, 2 ноль, А2). В этом случае все Подмножество ВВЙ ??, содержащее все пары ** (/) серии A2) С другой стороны, для некоторых / до пары вида *, (m,) pr С другой стороны, новая модель является оптимальной, а с другой стороны, После объединения групп элементов они преобразуются в наборы Нет. *? #?
- Какой из них лучше для оригинальной модели? Написать Сегмент из строки А2): … A3) 217 с того времени Po (.) = Po (. (L)) m, = 6 м (, Перейти Пл {х. A)) = _Pii? IL ^ IiM. a = _PiIM. а. Поэтому, учитывая А3), § Тот, который генерируется отношением A2) Заказ: Pi (Jty / Po K) ^ Pi K) / Po (*,)> •••. A4) Следовательно, оптимальное множество Wa, сформированное выше, имеет вид Это написано как: Где A / A определяется как A4) и A является уравнением (9). Следовательно, оптимальное множество Wa включает в себя точку x, Максимальное отношение правдоподобия Pi () / Po (*) — Позвольте мне объяснить то же самое для непрерывных моделей Большинство.
Где .V — некоторая точка D; i = l, …, N и b Незначительная ошибка в уравнении N. A6) От А5) и А6) A7) Использование разобранной разобранной модели с аналогичной вероятностью Возможно, тот же результат с возможностью для Po Ва построен из зоны А и имеет самый высокий вероятный процент Вероятность / i (x,) // o (x,), x, eE, -. Лемма 1 (Неймана а — Р и р, о и а). Для статистики Модель (8B, A, {Po, PJ) и гипотеза Ho: P = P0, H,: P = P Произвольная k область B7 * = {x: L, (x) / Lo (x)> A! } A8) (Где Li (x) — вероятность меры P, а «= 0, 1) — максимум Мощность между всеми областями W одинакового или меньшего размера: (P () A9) где B0)
Предполагая, что носитель плотности f0 (x) конечен, сломайте его Конечное число областей A /, i = 1, …, N, с объемом | D / | = b // o (x /), A5) Людмила Фирмаль
Выполните доказательство непрерывной модели. Пожалуйста, дайте мне E)) φ (x) и φ * (x) являются важными функциями W и W * соответственно. Думаю, функция (Φ * (x) — <p (x)) (Ex) — * Ex «. В xelV * оба фактора B1) не являются отрицательными: первый фактор φ * (x) = 1, как определено вторым -A8). x§F в Первый фактор в B1) -φ (x), Не позитивно, учитывая A8, второй фактор также не позитивен. В этом случае установите dx = dx \ … dxn и рассмотрите интеграл получить размер L как 0 0, то φ * (x) = 1 Значит φ * (x) -φ (x)> 0, а мало? G V и т. Д. fi (x) -kfo (x) 0. Следовательно, х ^. $ B OV, интегрировать функция (Φ * (x) -φ (x)) (Mx) — * Mx))> 0.
Итак, на практике эта функция равна нулю Почти все? EV как мера Лебега. Однако μ (x) -> 0 (x)> 0 на S8QV, так что φ * (x) = φ (x) почти все E? Так против почти всех хей? | Критерий W *, определенный в A8), называется критерием Вероятность отношений. Запомни это с продуманной статистикой Статистическая модель статистики Li (x) / L0 (x) дает минимум Достаточное разложение (подробнее см. §6§15, §3§16) Статистика критерия W * является наименьшей функцией Достаточно статистики.
Смотрите также:
| Метод Монте-Карло в модели сдвига-масштаба | Сложные гипотезы |
| Проверка статистических гипотез | Последовательный критерий отношения правдоподобий |
Если вам потребуется заказать статистику вы всегда можете написать мне в whatsapp.

