Оглавление:





Ламинарный пограничный слой на плоской пластине
- Массоперенос был изучен для бинарной смеси в ламинарном пограничном слое на плоской пластине. Мы рассчитали влияние массового потока, перпендикулярного результирующей пластине, на коэффициент массопереноса. Результаты расчетов приведены на рисунке. 34. 1. Обратите внимание, что этот массовый поток влияет на передачу тепла. Также видно, что это влияет на коэффициент гидравлического сопротивления. Эта глава расширяет результаты, полученные с помощью ч. 34, передача тепла и импульса основана на их аналогии. Подробные выводы не делаются.
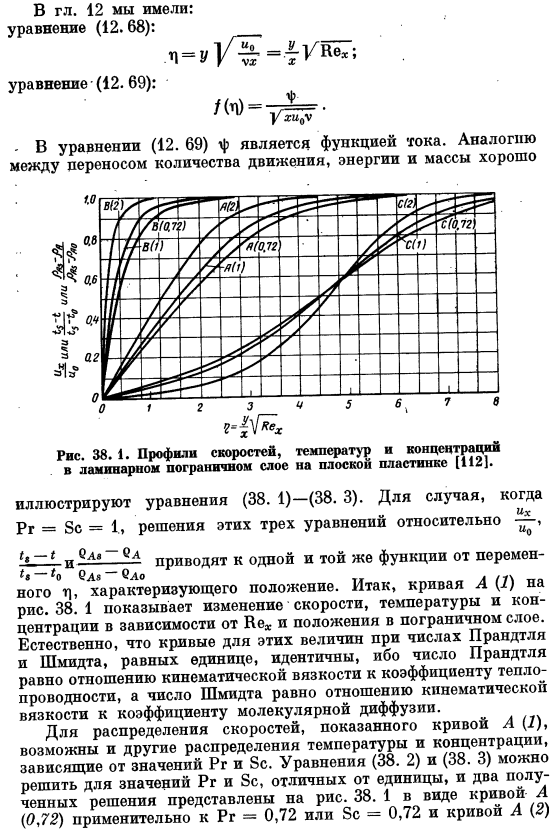
Начните с написания следующих уравнений для импульса, тепла и массопереноса в ламинарных пограничных пластинах, полученных в предыдущей главе. Формула (12. 70) и (12. 72), выглядит так: Из Формулы (24.3) Ваш 12 что у нас было: уравнение (12.68): Формула (12. Шестьдесят девять): /(Р)= — Д =. ■ Уравнение (12. 69), где φ-функция ка. Аналогии Передача импульса, энергии и массы хороша Рис.38. 1.Профили скорости, температуры и концентрации ламинарного пограничного слоя на плоской пластине [112].
Разница в весе ребра с такими вогнутыми поверхностями и ребра треугольного сечения очень мала. Людмила Фирмаль
Формула (38.1) — обозначает (38.3). Если Pr = 8c = 1, то решение этих 3 уравнений относительно −5 и^ * _ ^приводит к одной и той же функции переменной r |и характеризует положение. Таким образом, кривая рисунка а (7) 38. На рис. 1 показаны «изменения скорости, температуры и концентрации» в зависимости от положения вехи и пограничного слоя. Поскольку число Прандтля равно отношению кинематической вязкости и теплопроводности, а число Шмида равно отношению кинематической вязкости и коэффициента молекулярной диффузии, естественно, кривые для этих величин идентичны, когда число Прандтля и число Шмидта равны 1.
Для распределения скорости, показанного на Кривой A (I), возможны другие распределения температуры и концентрации в зависимости от значений Pr и 8c. Формулы (38.2) и (38.3) могут быть решены для значений Pr и 8c, отличных от 1, и полученные 2 решения показаны на рисунке. 38. Pr = 0.72 или 8c = 0.72 и 1 формы кривой A (0.72), примененной к кривой A (2) Применяется к Pr = 2 или 8c = 2.Например, в случае пара пентана, рассеивающего слоистый пограничный слой воздуха от нагретой пластины, Pr pr 0.7 A и 8s R 2.0.
Определяется Кривой A (I) — Кривой A(0.72)、 По А—А-Крпв ° (2).Как упоминалось ранее, для водяного пара, диффундирующего через слой воздуха из нагретой пластины, PR = 0,72, 8C немного меньше 0,72.Кривая а (0,72) почти отражает как температурный профиль, так и профиль концентрации. Число Льюисов в этой системе приблизительно равно Равно 1. Мы обнаружили, что массовый расход поверхности пластины, характеризуемый вашей 34-й безразмерной группой / * * exVex, существенно влияет на форму кривой на рисунке. 34.1.Это также показано на схеме. 38.
- Группа в принимает существенно отличное от нуля значение либо из-за большой разницы в концентрации, либо из-за притока или оттока жидкости через поры пластины. Кривая B 38.1 на рисунке применяется, когда вещество движется от потока жидкости к пластине со скоростью, аналогичной C | ’* = −2.5.Кривая С Вещество переносится из пластины в поток, что актуально в случае B|, ’ UVE ’ = 1,0. О Где Рисунок 1 38.Распределение концентрации по скорости, температуре и коэффициенту переноса пропорциональна наклону кривой на рисунке.
Эти Паклоны используются для определения локального фактора точки. «^BBe, x является постоянным по длине пластины. См. уравнение (34.5).Поправка среднего коэффициента по всей длине пластины b равна поправке коэффициента точки. При передаче импульса коэффициент гидравлического сопротивления рассчитывается по формуле (12. 81). С-2Ра-2X1、 Люди » е」 Где локальное значение t поверхностного напряжения сдвига. Формула (12. 76) по этому значению Уравнение (12.81) и (12.76) в совокупности、 Формула (12. 68), используя определение [m]и выражение (38. 4) переписать. Производная формулы (38.6) может быть получена из наклона кривой A (I), B (1) и C (7) при r)= 0. 38. 1.
Для построения контура сечения ребра с постоянным тепловым потоком можно использовать любую часть окружности, как показано пунктирной линией. Людмила Фирмаль
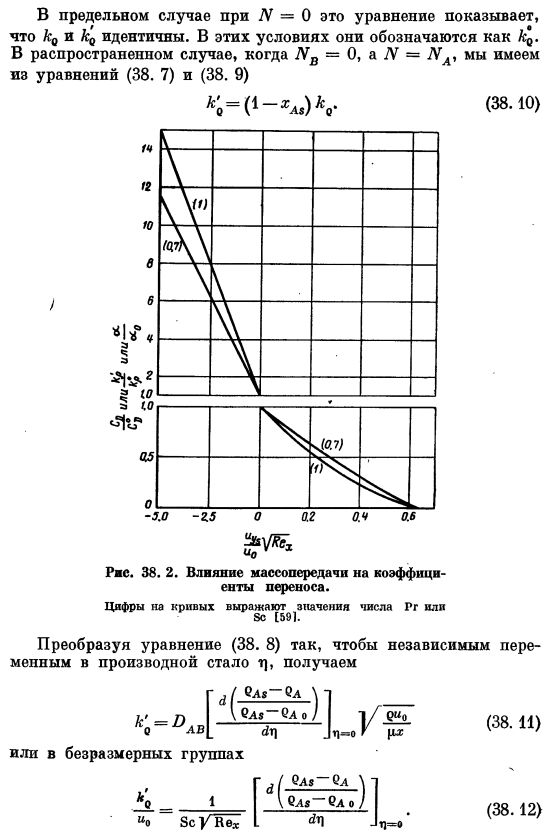
Понятно, что коэффициент гидравлического сопротивления сильно зависит от массообменного комплекса-эффекта Последний из со обозначен кривой (I) рисунка. 38.2; Co соответствует значению u = 0. На рисунке показан коэффициент массопереноса k ^ 38.2 A ’ Формат проведения、 (38.7) Поток и N-это альфа (y = 0) streams. By уравнение (34.7)、 ⁽⁽⁽ Формула (38. 8) представляет собой формулу (38. 4) и тому подобное. Однако гл. мы использовали коэффициент 33-37. (38.9) Q и K relationship отношение, уравнение (38. 7) и (38. 9) вы можете получить путем объединения. К ⁰ Если N = 0, то это уравнение указывает, что q и cd идентичны. В этих условиях он обозначается как cd.
В общем случае LGW = 0 и N = 1UL формула(38. 7) и (38. 9) от к’Д ^ — х ^ к’. (38.10) (38.И затем) (38.12) Формула (38. 12), где производная рассчитывается от наклона кривой на рисунке. 38. На рис.1 показано влияние массопереноса на коэффициент k’o. результаты также показаны на рис. 34. 38. 2.Параметры (0.7) и (7) — это число Шмидта. Приведенное выше уравнение массопереноса также может быть выражено коэффициентами kx, K% и др. Коэффициент k°равен значению k ’, если im = 0. 1 компакт-диск?
Она получается на основе k’o по формуле для b = 0(38.10). Коэффициент теплопередачи A. рисунок 38.2, определяемый зависимостями (24. Пять): Последнее уравнение можно свести к форме отношения между неразделенными бандами, и обе части можно разделить на слио. (38.14) (38.15)) Производная формулы (38.15) определяется по кривой рисунка. 38.1; обе функции Pr и Tsu * e*.Кривая на рисунке 38. 2 применяется к теплопередаче, если параметры (0.7) и(1) считаются числами Прандтля.
Смотрите также:

